Viveckh's Notepad

# Examples

  • Fast modular exponentiation algorithm
  • Euclid's GCD algorithm

# Merge Sort

Best Video showing it in action

Code

# Gauss's idea

This isn't necessarily a D&C concept but can be used while solving fast multiplication D&C problem

Multiplication is expensive , adding/subtracting is cheap

To get the product of two complex numbers: and

(a+bi)(c+di)=ac+adi+bci+bdi2=ac+adi+bci−bd=ac−bd+(bc+ad)i (a+bi)(c+di)=ac+adi+bci+bdi^2 =ac+adi+bci-bd=ac-bd+(bc+ad)i

Since there are four products of real numbers involved (ac, bd, ad, bc), can we lower the number of multiplications?

We can do so by computing (bc+ad) directly without doing the multiplication bit for that part.

Elaboration

Reusing this in the above equation of multiplying two complex numbers, we get

So, due to the modification, now if we compute three real number multiplications: ac, bd, (a+b)(c+d), we can now get product of two complex numbers.

# Fast Multiplication

Multiplying two N-bit numbers where the numbers are large like 1000-2000 bits, we can't use the simple multiplication since the hardware can't handle it. For things like RSA.

Input: n-bit integers X & Y, assume n is a power of 2 Goal: compute running time in terms of n

# Naive Approach

fast-mul-naive-recursive.png

Above, the way X is and is a formula. The same is being done for Y as well

fast-mul-naive-code.png

Run time:

Look at Solving Recurrences to understand how this solves to

# Improved Approach

This is where we simplify the above approach using Gauss's idea. We apply Gauss's idea to the part where XY is expressed in terms of , , , . Instead of having four multiplications, we can lower that expression to only have three multiplications.

fast-mul-improved-approach.png

fast-mul-improved-code.png

Run time:

The runtime of this improved approach is explained here

# Median

Finding median from a large list of unsorted numbers

A trivial solution with O(nlogn) time complexity is sorting the list and choosing n/2 item for median. But we want something more efficient at O(n)

We are going to leverage a modified version of Quicksort algorithm for this.

# How quicksort works

  • Choose a pivot p (main challenge)
  • Partition A into
  • Recursively sort

The time complexity for quicksort is O(nlogn) but we are going to aim to make it efficient.

# Finding n-th largest element

See below for how we'd pick the n-th largest (k) item using quicksort without fully sorting

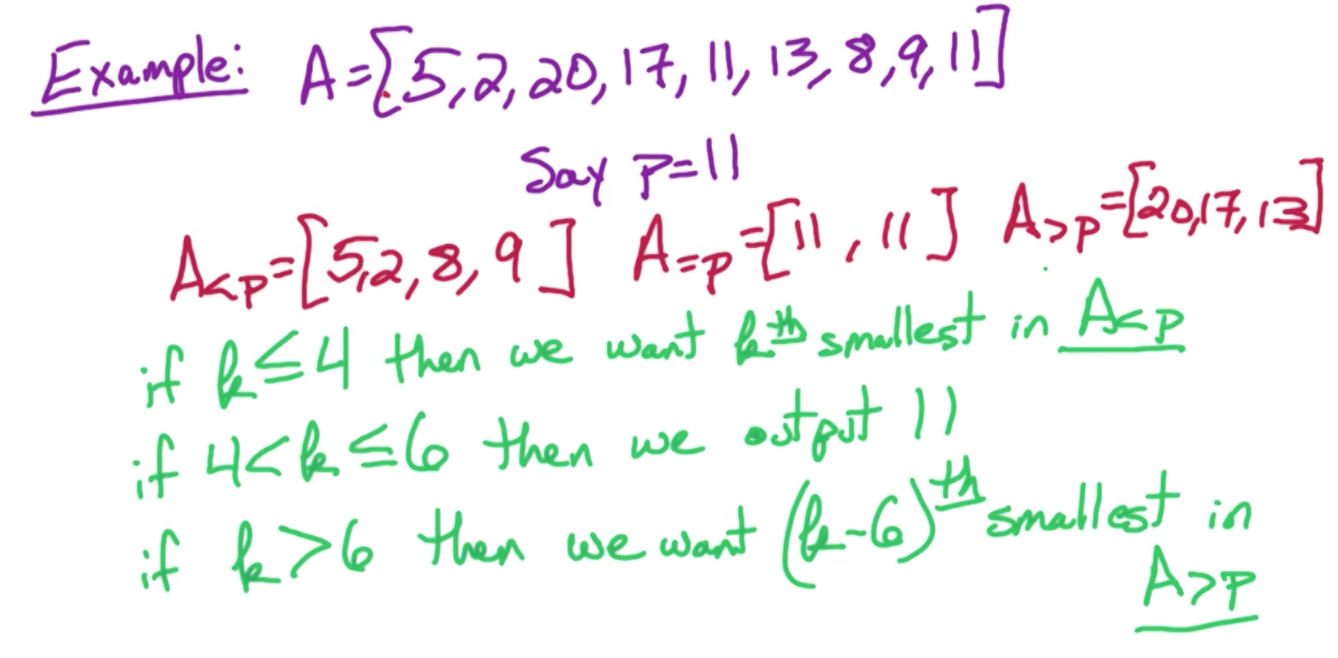
nth-item-using-quicksort.png

As we can see above, after we partition, we only sort or just take the A == p depending on which bucket contains our index of interest. In case of a median, we're interested in k=n/2. So after such a partition, we only zoom in to the bucket that has that index. And we only sort that bucket, and get the value from the index. In the case above, we'd just pick the A==p since it has index 5 and 6 and we'd just pick 11 from there. Of course, the main challenge lies with how to pick the best pivot for partioning.

Expressing the above in psedudocode form looks like this:

quickselect.png

To achieve an efficiency, we need this expression to be such that a < b. So if a is 1 since there is only 1 sub problem, we need to ensure b continues to be greater than 1. 1/b part of the equation dictates how much smaller the input list becomes with every iteration, this means, even if it is not sufficiently small like 1/2 (where b=2), that's fine. We have values like 3/4 (where b = 4/3) and that is fine too, it will still ensure our overall time complexity gets resolved to O(n) using master theorem.

Good Pivot: Therefore, a pivot p is good if .

This will ensure a runtime of

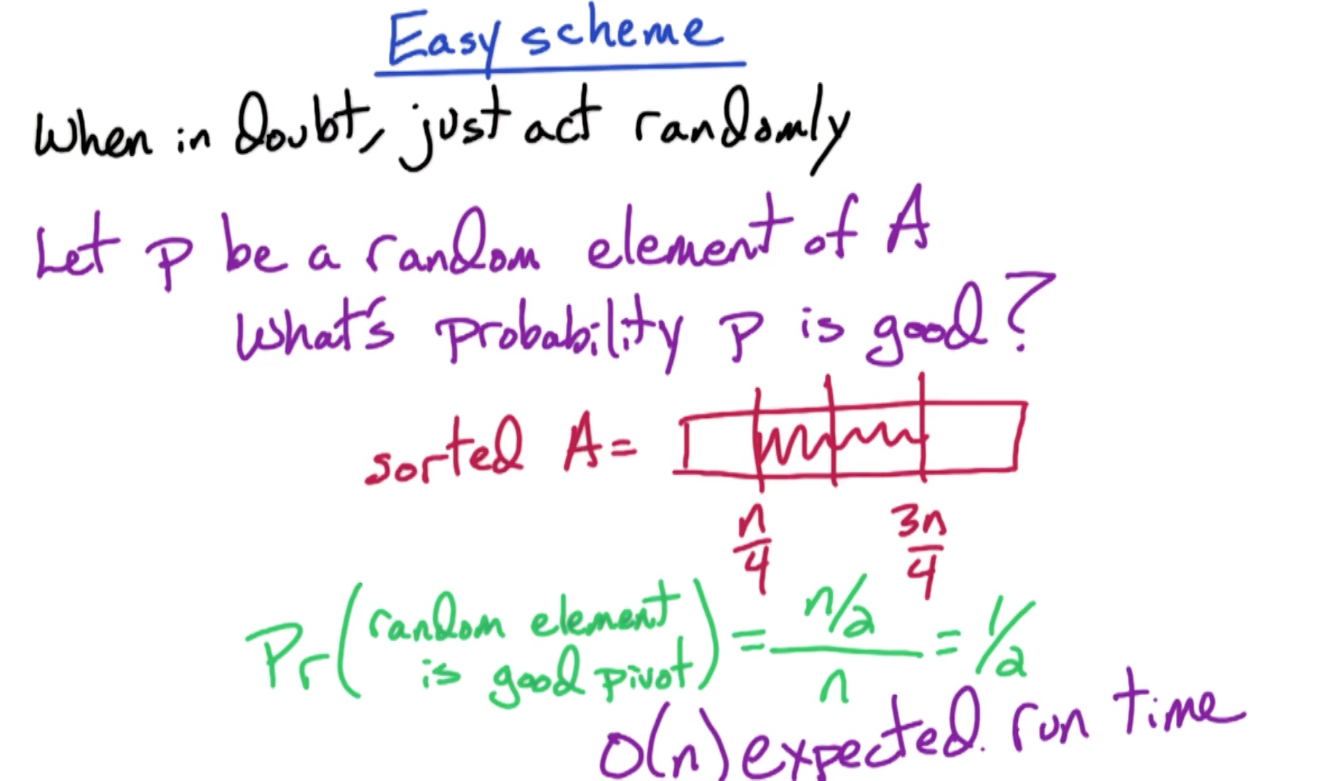
# Good Pivot

We can pick a random pivot and still have a 1/2 probability we will make a good pick, because to fulfill the above runtime, we just have to pick something between and . But this only yields an expected run time of O(n) not guaranteed.

pivot-random.png

A better approach is outlined below. If we can aim for the sub-problem input size (1/b) to be th (0.75) the original size, we still have 0.24 left before 1/b becomes 1 and a < b is not true anymore. So we can use that additional bandwidth to find the pivot.

pivot-recursive.png

Bad approach: The following shows why choosing the first n/5 elements of A as the subset S is not a good idea. Lets assume A is sorted, then choosing S as the first n/5 elements of A means:

  • S = n/5 smallest elements of A
  • P = n/10th of smallest element.

So the subproblem doesn't decompose by much as most of the partitioned elements fall in the ` bucket.

Good Approach: We need to choose S such that it is a representative of A. We want median(S) to approximate median(A).

  • Break A into n/5 groups of 5 elements each. (choosing 5 because we have to do this using the extra bandwith discussed above to still be at O(n) runtime collectively. We can only break up problems so subproblem input is 1/5 of original input)
  • For each group:
    • Sort the elements within each group and take the median of each group (performance boost here in sorting since this is O(1) due to each group having too small number of elements)
  • Continue this recursively and eventually we get a median.

# Pseudocode

fast-select-pseudocode.png

fast-select-runtime.png

# Fast Fourier Transform (FFT)

# Useful resources

Good Set of slides

Concise Explanation by Sai Sandeep

# Problem Definition

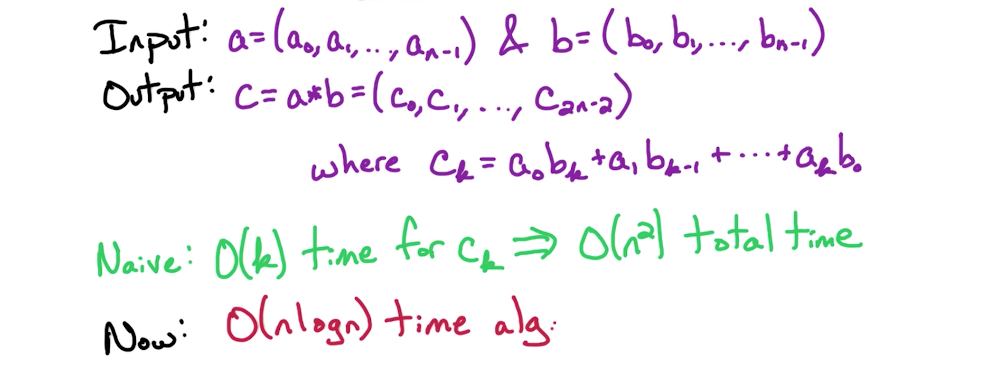
poly-mult.png

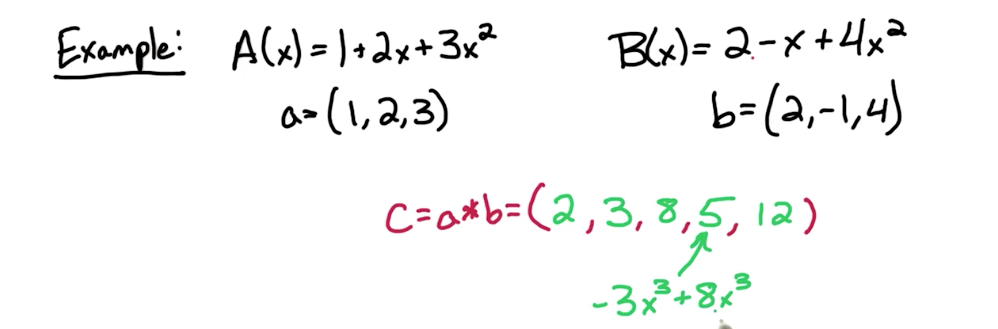
poly-mult-example.png

# Polynomial basics

poly-basics.png

FFT allows us to convert from coefficient-form to values-form and vice versa. The benefit of values-form is polynomial multiplication is more efficient in this form, but the benefit of coefficient-form is a convenient/better way to represent a polynomial. Important point to note is that FFT converts a polynomial from coefficients to values but not for any choice of x1...xn but for a particular well chosen set of points, x1...xn. Now what points do we choose? That's the beauty of FFT explained below in FFT: Opposites section and Complex Roots We can compute

To validate how Lemma works, lets think of a Line. A line is a degree 1 polynomial (mx + c has only 1 power to x), so it can be represented by 2 points. A triangle is a degree two polynomial and can be represented by 3 points.

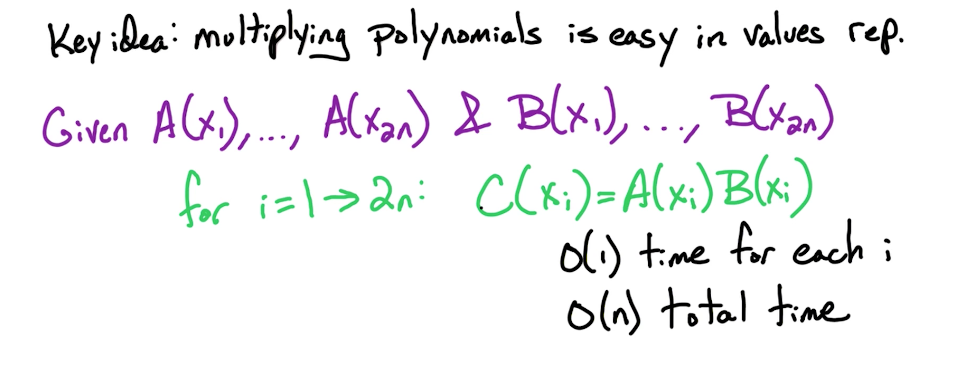
poly-mult-key.png

A and B have to be padded before multiplication so it has enough degrees as there would be in C after multiplication.

# FFT Opposites

fft-opposites.png

+- property: are opposite of

# FFT Even & Odd

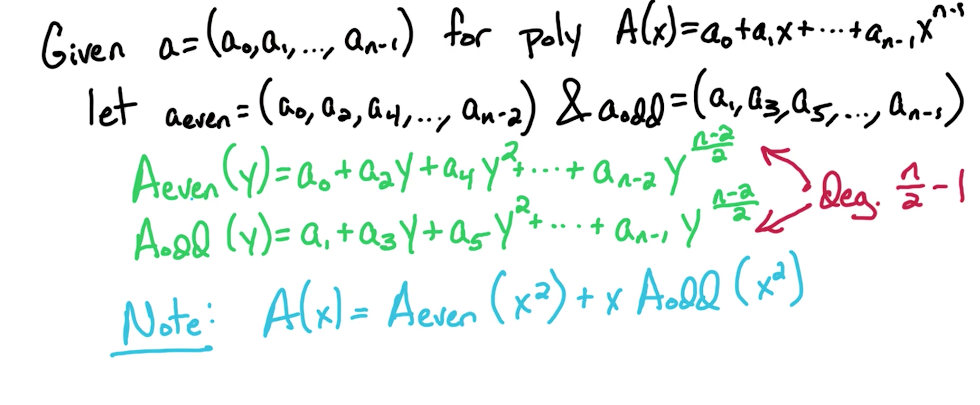
fft-even-odd.png

We split the odd and even items from the polynomial. When split, we use the powers of y in the splits to express continuous power. So basically, in A_{even} becomes

# FFT Recursion

fft-recursion.png

# FFT Summary

fft-summary.png

# FFT Algorithm Pseudocode

fft-highlevel.png fft-pseudocode.png fft-core.png fft-complexity.png

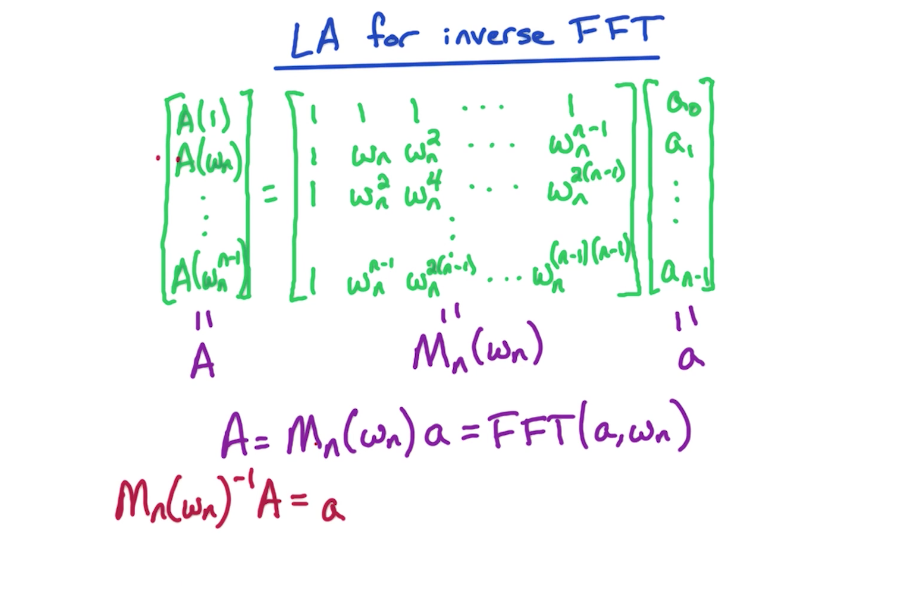
# Linear Algebraic View

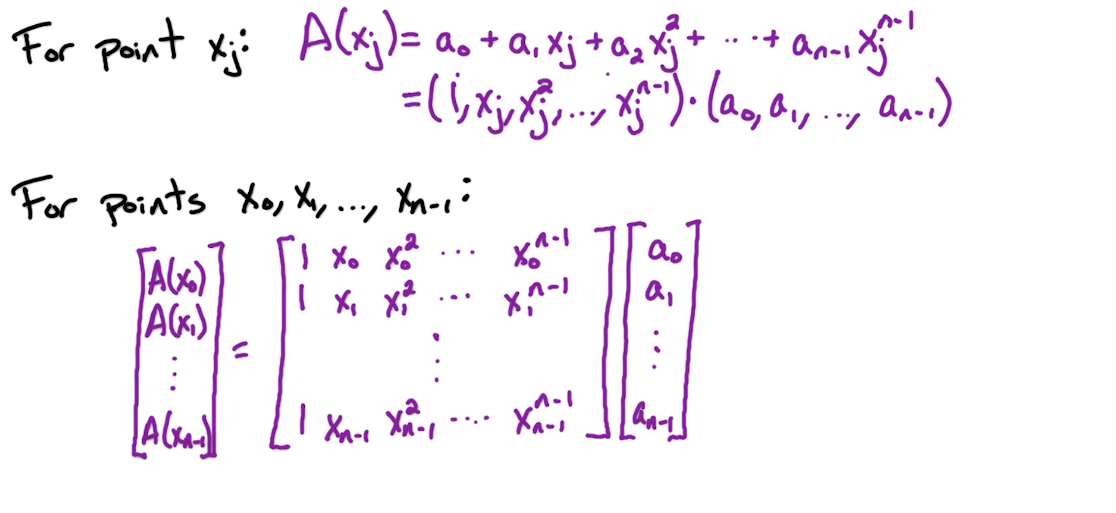
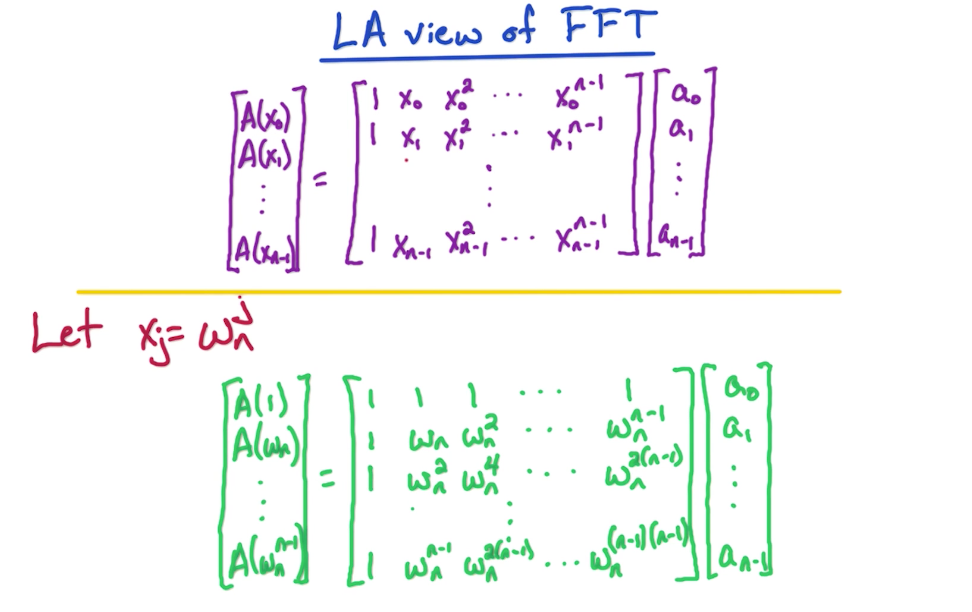
fft-la1.png fft-la2.png

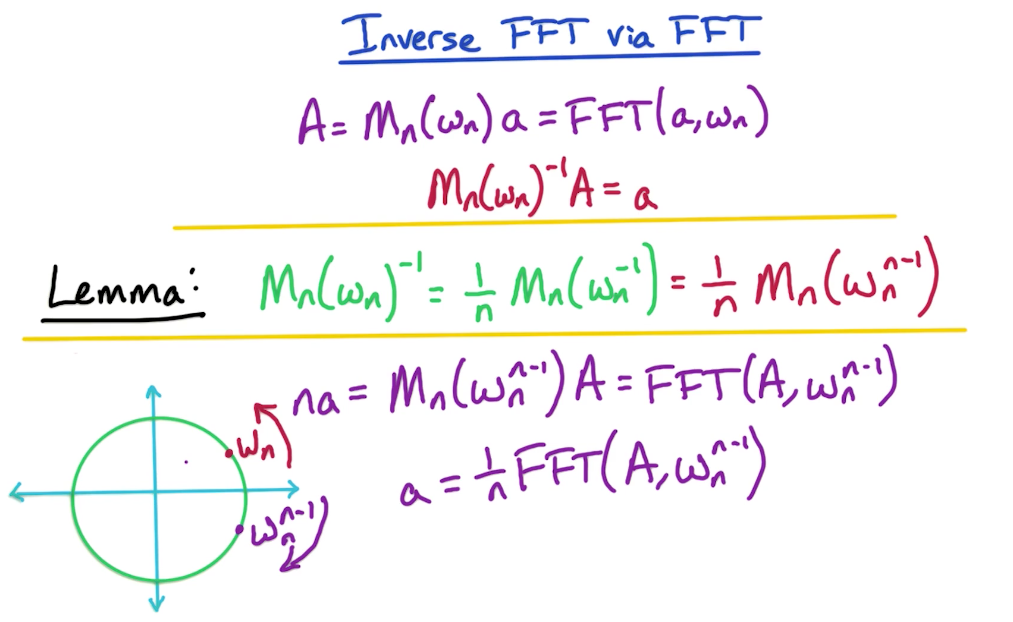
# Inverse FFT

In the first line below, we see the way we compute FFT. Then after that we are modifying that same equation to yield inverse FFT but using the same function fft-inv-formula.png fft-inv-la.png

# Complex Numbers

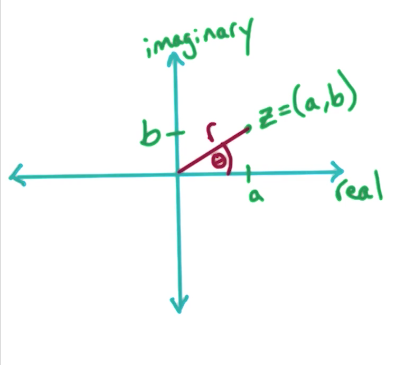
# Polar coordinates

A complex number is expressed in the complex plane as and expressed in the polar coordinates as

Euler's Formula:

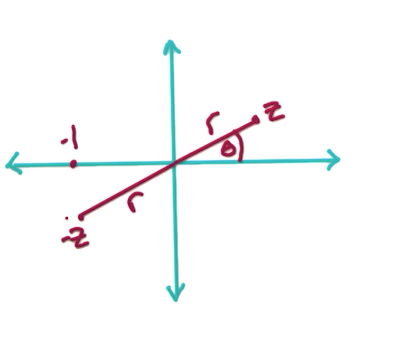
Polar coordinates are a better representation for our purposes for multiplication.

polar-coordinates.png

Polar is convenient for multiplication

If we want to compute, , we would do the following

polar-mult.png

# Complex roots

n-th complex roots of unity are defined as those numbers z where

Examples

Deriving formula for n-th root

since and

can also be written as

so this means,

Therefore, n-th roots of unity can be computed so that r is always going to have a constant value of 1, and the theta is going to change based on the value of n which would be problem-specific, and j which is going to be sequential . So, all the n-th roots of unity would fall in a circle.

Below is an example of computing 8-th roots of unity.

Notice that there are n-distinct values, and after hitting n, the values would start to repeat since the roots are in a circle.

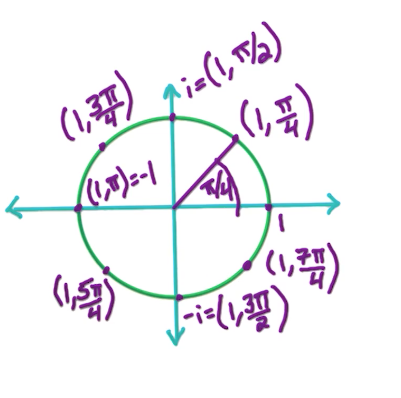
8th-root-of-unity.png

The n-th roots are represented using . In the example above,

  • and likewise

Formula 1: Making the general form to be where .

Tip: If a question asks to compute without a j value, assume the question wants to know j=1 since j=0 results in a zero angle anyway and is useless.

Basically, we divide the circle into n pies (think pie chart) and that is the visual representation of the n-th roots of unity. If you need to get lets say n + 1 or 2n roots, then you just loop over this circle again and again. In the visual example shown above where we got 8th roots of unity, .

Formula 2: Another useful formula of +- property is:

Formula 3: Using Euler's formula from above,

Below we can see how the different roots compare to each other for the various values of n, and also reflections of one another.

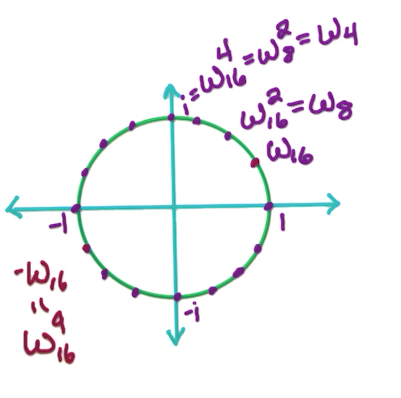
16th-root-of-unity.png

Tip: If lets say is to be computed, just compute the reflection of . To do this, compute omega angle by forgetting about the negative sign. And when computed the omega angle, visualize its reflection in the circle. This trick is useful for Q3 in the practice questions below. Also, on a separate note, another useful conversion is

# Key properties

The key properties of n-th roots of unity that we utilize are below.

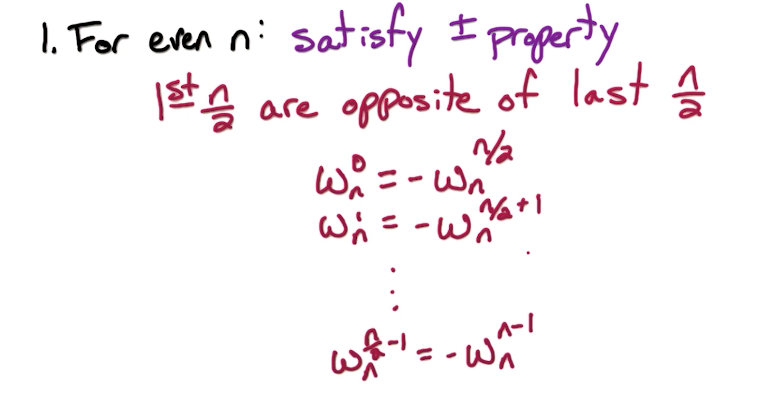
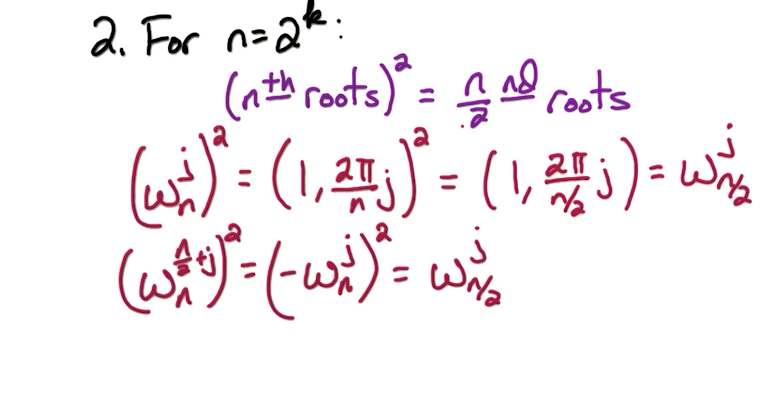
nth-roots-property-1.png nth-roots-property-2.png

# Complex Roots Practice

Complex roots practice

# Solving Recurrences

# Expanding out

expanding-out-1.png

Note: While expanding out, don't simplify the power of something and leave them as is. This helps create the geometric series later to solve.

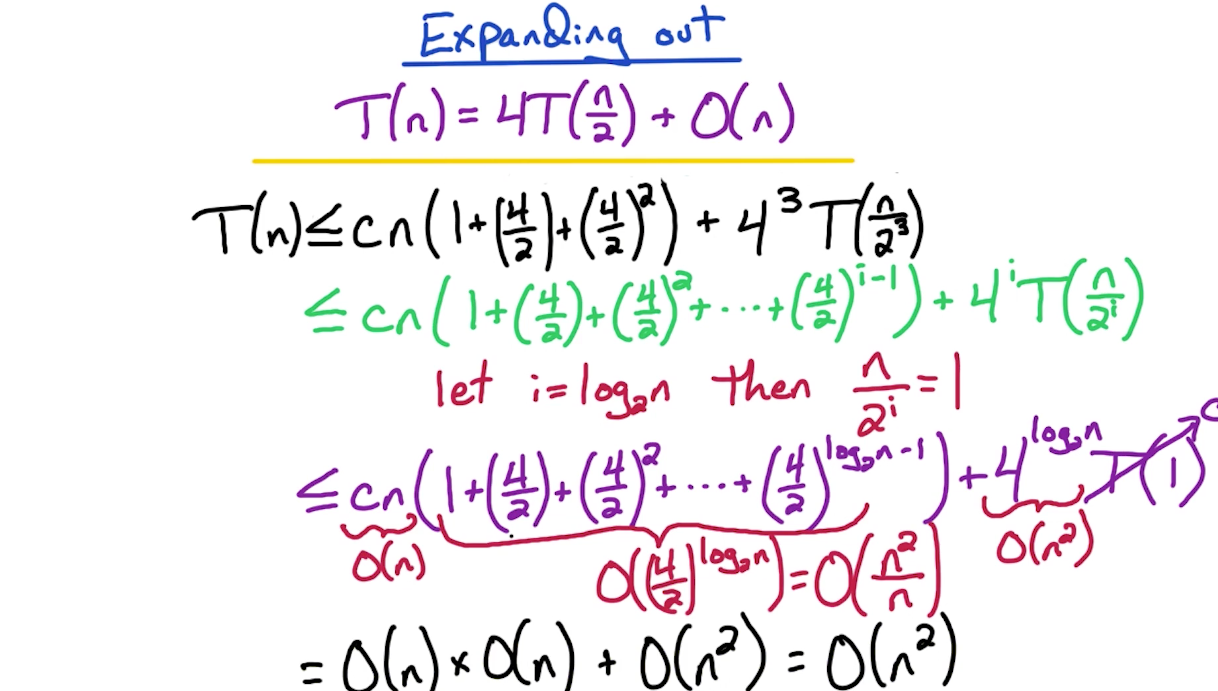
expanding-out-2.png

Notes:

  • When do we stop expanding? We stop when the expression inside T(?) becomes base condition i.e. 1. In this case, when . This happens if .

Proof

  • The has suddenly arrived by using the formula/mapping/technique described below in Geometric Series section. You might notice the power should be but that -1 is ignored since it is insignificant while converting to big O terms. Once that is done, it is eventually convered to O(n) using this breakdown:

  • The second half is solved by the technique described below in the Mapping polynomial section. On a separate note, the previous bullet point also attempts to solve a similar thing, for which we can use the same understanding of how logs operate.

# Geometric Series

geometric-series.png

  • The alpha > 1 scenario is seen in the recurrence analyzed above for the Naive Fast Multiplication.
  • The alpha = 1 scenario is seen in merge sort
  • The alpha < 1 scenario is seen in median finding

# Manipulating Polynomials

manipulating-polynomials.png

We want to express polynomials in form for Big O notations. Above, we are showing the process of expressing in big o notation

To do so, since the base of log is 2, we want to convert the overall polynomial from the form to the form.

To do this, 3 can be written as . Substituting this in the original polynomial, we can eventually convert it to

So quick calculation can also be done like this =

# General Recurrence

general-recurrence.png

# Examples

# E.g. Merge sort

We partition the list to two: each of n/2, and sorting each is T(n/2). Since there are two partitions, it becomes 2T(n/2). Then merging it back takes O(n).

# E.g. Fast Multiplication: Naive

  • Had 4 subproblems, therefore 4T
  • n items were divided to n/2 each time, and hence the n/2.

# E.g. Fast Multiplication: Improved

  • Had 3 subproblems, therefore 3T
  • n items were divided to n/2 each time, and hence the n/2.

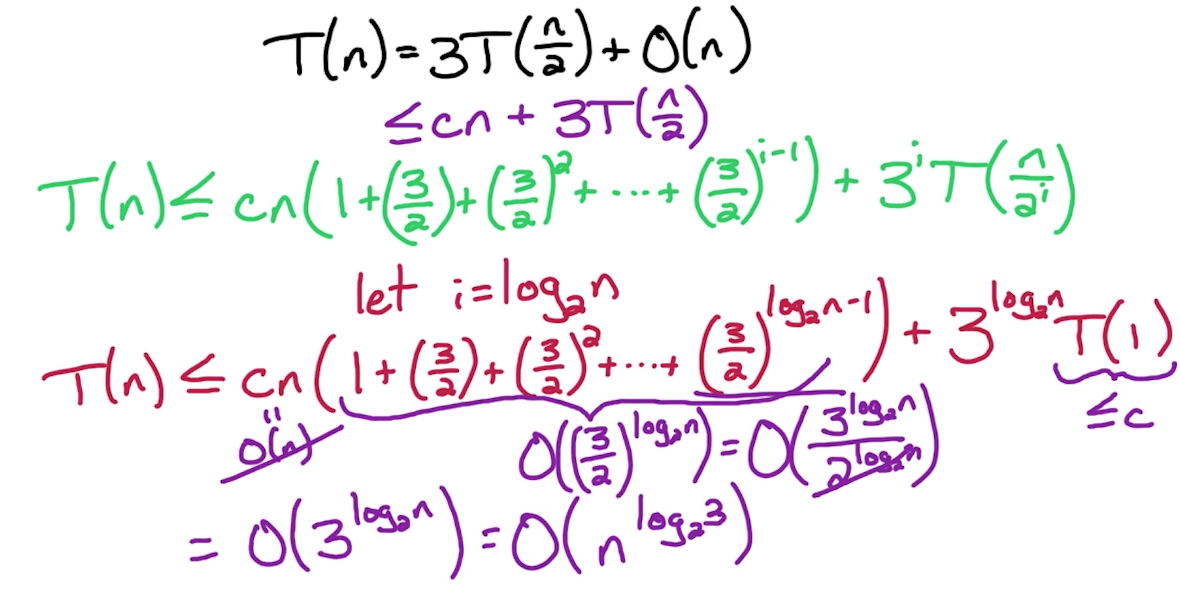
fast-mul-improved.png

# E.g. Median

Runtime:

← Math →