Viveckh's Notepad

# Modular Arithmetic

Modular arithmetic is the foundation on which RSA is based.

For integer :

= Remainder when x divided by N

means x/N and Y/n have same remainder

mod-3-ex.png

# Basic Fact

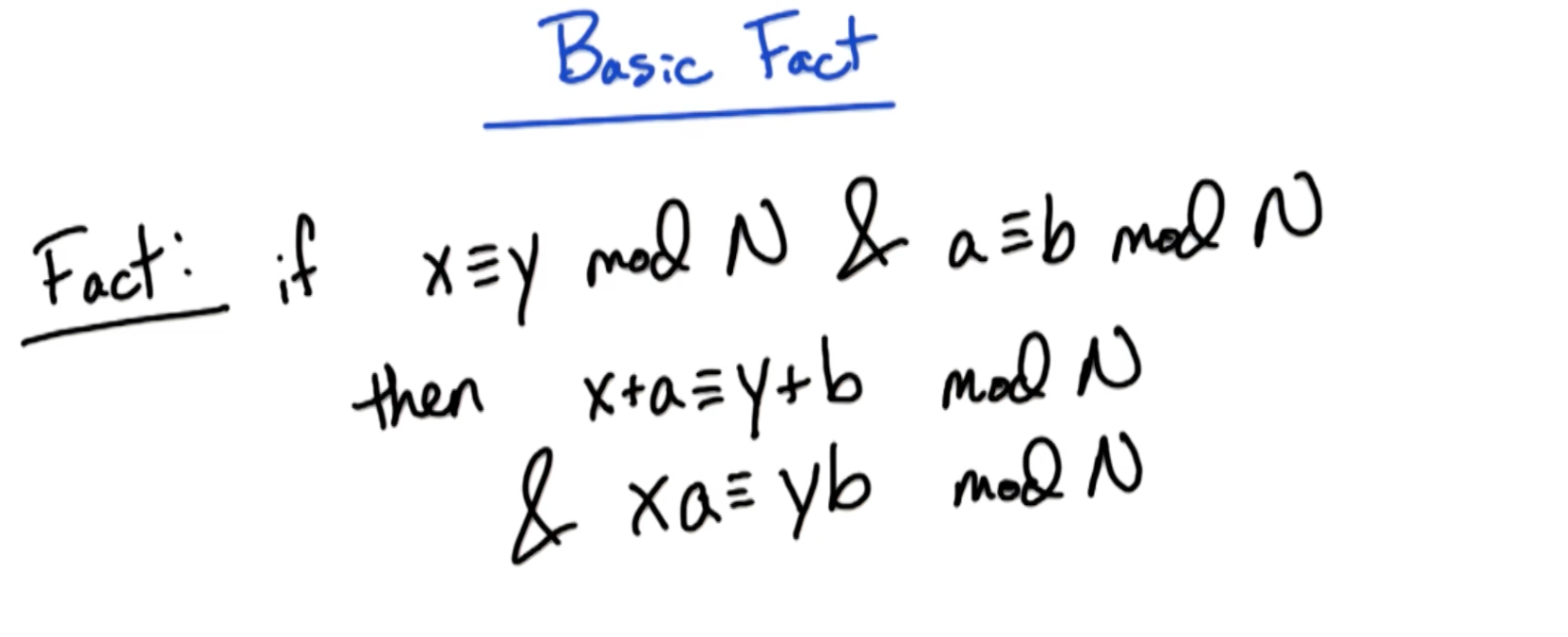
basic-fact.png

The above fact comes in handy to simplify and solve cases like the following:

321 x 17 mod 320

321x17.png

# Modular Exponentiation

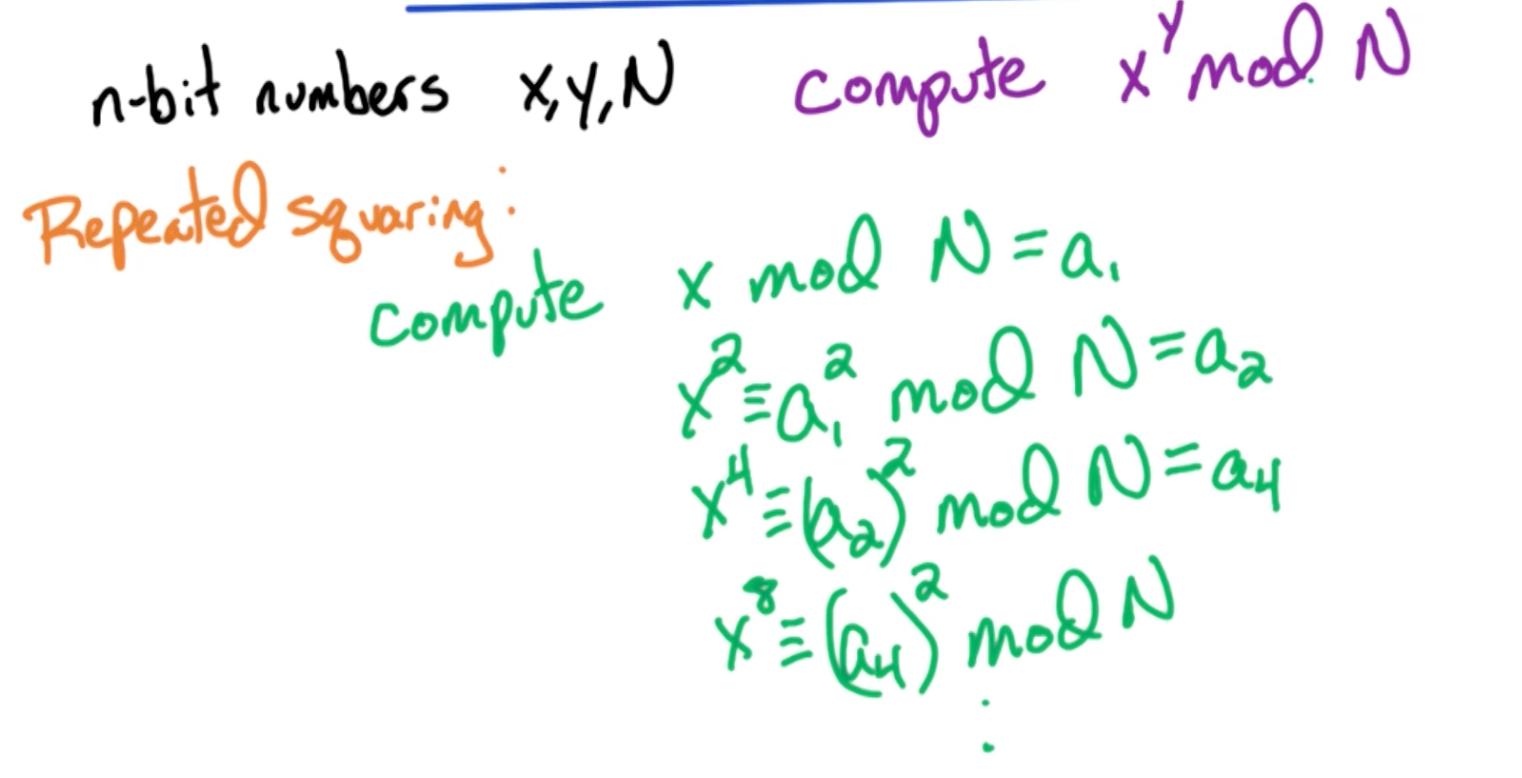
mod-exponentiation.png

Example:

mod-exponentiation-ex.png

# Mod Ex. Algorithm

mod-exponentiation-algo.png

# Multiplicative Inverses

mult-inverse.png

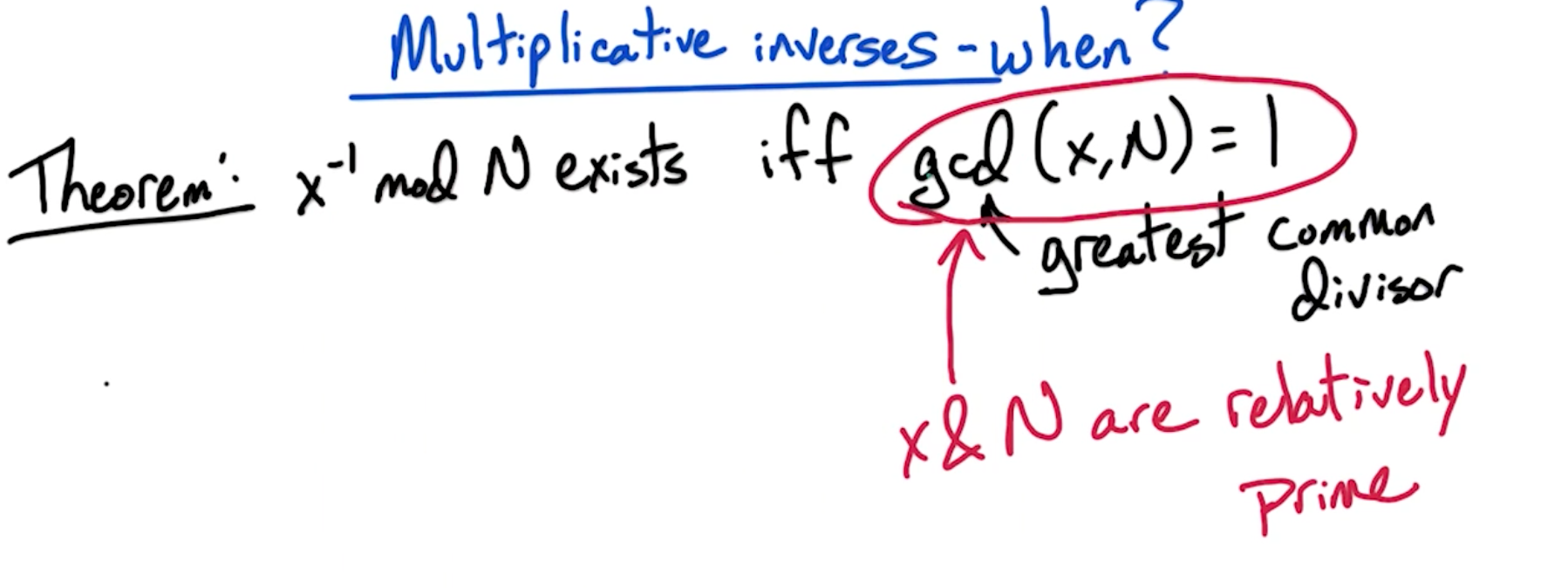
mult-inverse-when.png

Multiplicative inverse of x exists iff the greatest common divisor of x and N is 1. This is also referred to as x and N being "relatively prime".

# Euclid's GCD Algorithm

euclids-algo.png

The running time of this algorithm is

# Extended Euclid's Algo

For computing multiplicative inverses

ext-euclids-algo.png

The running time of this algorithm is

Using extended Euclid's algo, compute

ext-euclids-algo-ex.png

# RSA

# Fermat's Little Theorem

fermats-theorem.png

# Euler's Theorem

It is a generalization of Fermat's little theorem.

eulers-theorem.png

For a prime number P, (since every number upto p are relatively prime to p)

# Euler's Theorem for N=pq

Likewise, for primes p and q, let N = pq.

In this case,

Therefore, for any z, where then,

And this is the fundamental idea that powers the RSA

# RSA Protocol: Receiver I

  • Bob picks 2 n-bit random primes p and q
    • This can be done by randomly generating a n-bit number and primality testing it
  • Bob chooses e relatively prime to (p-1)(q-1)
    • This means using Euclid's Algorithm
    • Incrementally try with e=3,5,7,11...
    • Let N = pq
  • Bob publishes his public key (N, e)
  • Bob computes his private key:
    • We know d exists because e is relatively prime to (p-1)(q-1)
    • We can compute d, using extended euclid's algorithm

# RSA Protocol: Sender I

Alice wants to send message m to Bob

  • Looks up Bob's public key (N, e)
  • She computes using fast modular exponentiation
  • She sends y

# RSA Protocol: Receiver II

  • Bob receives y
  • Decrypts y by computing to retrieve the original message, m

# RSA Pitfalls

When the encrypted message is computed,

  • If p divides m and p divides n, then p will also divide y. In such a situation, a hacker can simply compute, and get p since y is the encrypted message itself that is available, and N is part of public key. And then they can find q since hence gathering all the info necessary to compute private key d and decrypt the message m.

  • m not too large

  • m too small

  • Sending same m, e times - if the hacker can see all those encrypted messages, they can derive it.

# Practice Q

Given p = 13, and q = 31, what is the smallest encryption key and public Key (N, e)

The smallest encryption key e = 7.

Why? and e = 3 and e = 5 are not relatively prime to 360 (i.e., and ).

Therefore, the next smallest prime is 7.

Public key

# Primality

Random primes are generated by randomly generating 0/1s for each bit of a n-bit number and checking if the overall number is a prime. Since primes are densely packed, we can expect to come across a prime number eventually after a few tries. However, the challenge is checking if the number is prime or not. And below is the discussion for it.

# Fermat's Test

fermats-test.png

# Better Primality

primality-test.png

← Graph Theory →