Viveckh's Notepad

# Connectivity in Graphs

Great Article Explaining the concept and properties

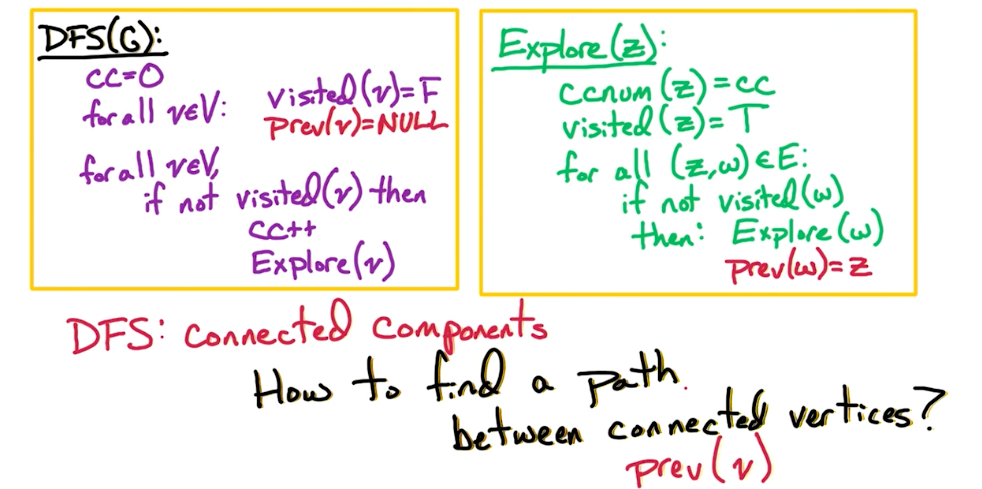
# DFS on Undirected Graphs

connected-comp-undirected.png

To find a path between connected vertices, we can use a prev object that gets populated as we traverse the graph with DFS.

connected-comp-undirected-path.png

# DFS on Directed Graphs

The general algorithm is the same as for undirected graphs, but instead of using the component number (cc), we use the pre/post order numbers. For connectivity algorithms, we're simply using post order numbers and not pre order numbers.

connected-comp-directed.png

An example of running DFS on a directed graph is below.

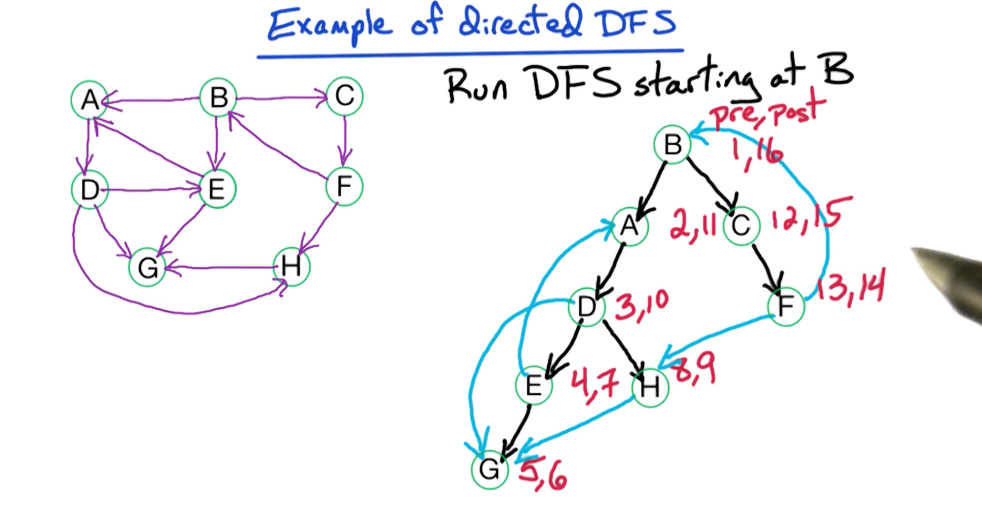
directed-dfs-example.png

The blue lines below are not really edges, they are just left there to show paths that were ignored because a node was previously explored already.

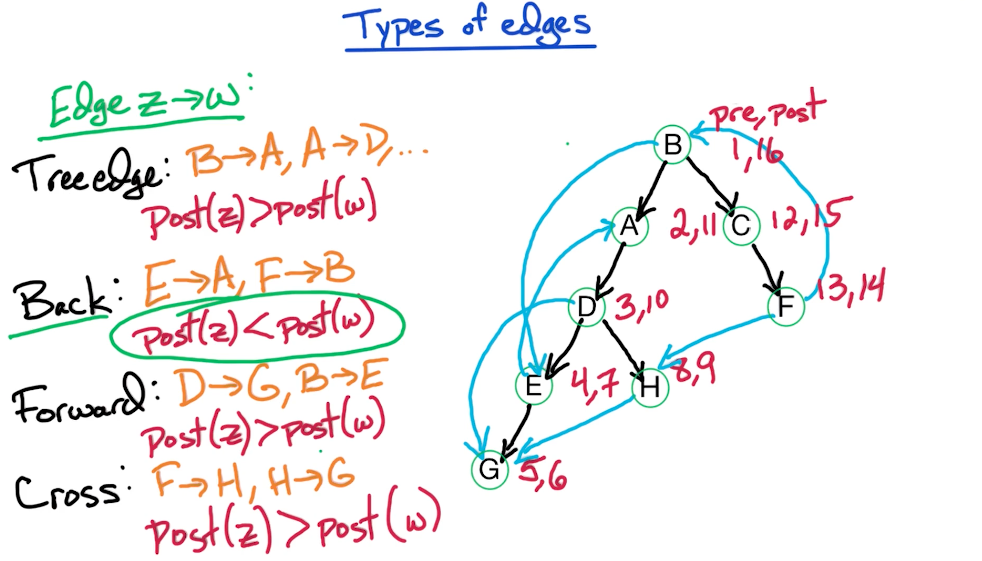
directed-dfs-types-of-edges.png

Tip: G has a cycle iff its DFS tree has a back edge

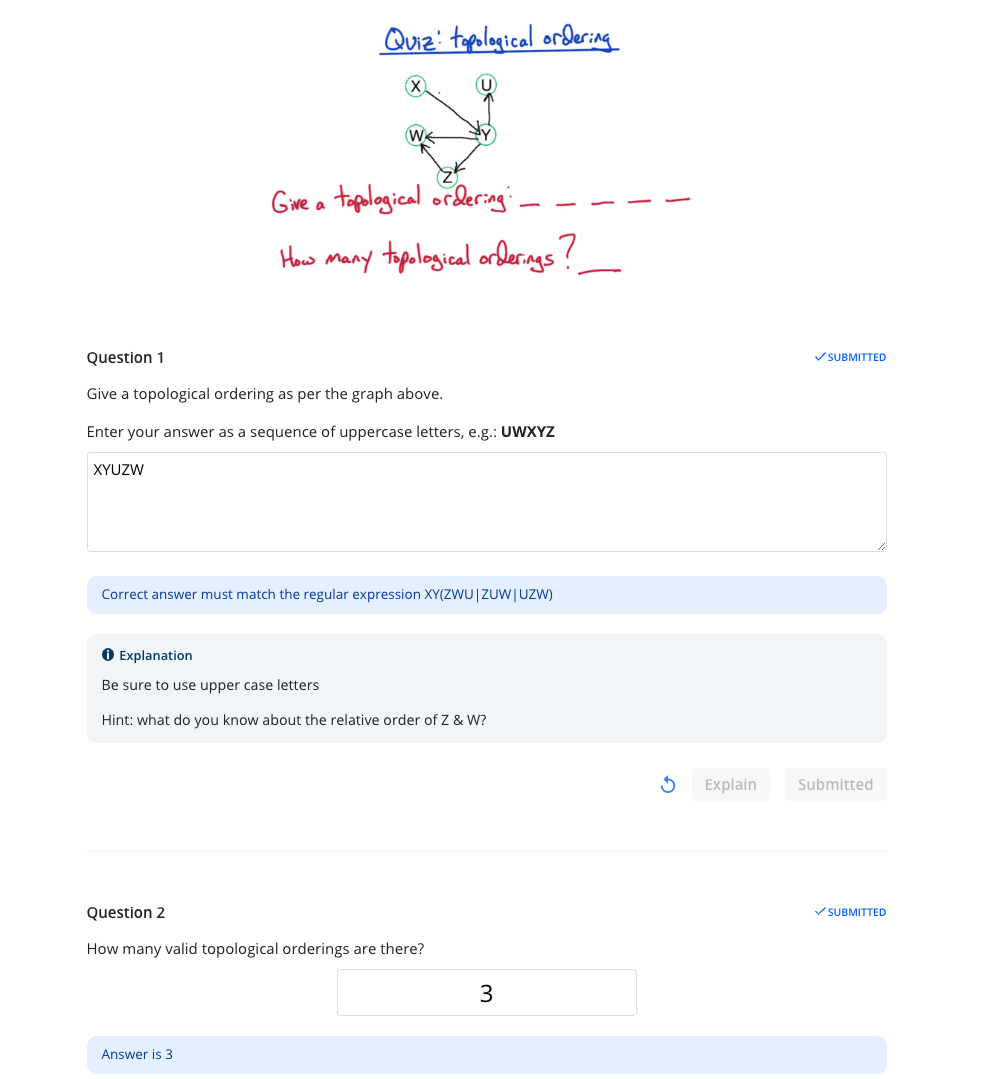
# Topological Sorting

DAGs are directed acyclic graphs i.e. no cycles i.e. no back edges.

Topologically sorting a DAG = order vertices so that all edges go from lower order number of vertex to higher.

  • Run DFS on DAG G: O(n+m)
  • for all , we know since there are no back edges, so order vertices by decreasing post order number: O(n)

The post order numbers can be in the range of 1 to 2n, so we can make an array of size 2n to hold the values.

The running time of the algorithm is linear O(n+m)

topological-sorting.png

# Source and Sink Vertex

  • Source Vertex = no incoming edges = highest post order number (imagine root)

  • Sink Vertex = no outgoing edges = lowest post order number (imagine lowest leaf)

# Alternative Topological Sorting Algo

  • Find a sink, output it, and delete it
  • Repeat the above until graph is empty

# Strongly Connected Components

Vertices v and w are strongly connected if: there is a path and

Note that there might be several vertices along the way between these two vertices.

In simple words, a strongly connected component (SCC) is a set of vertices in a graph such that you can get from any vertices to the other within this set.

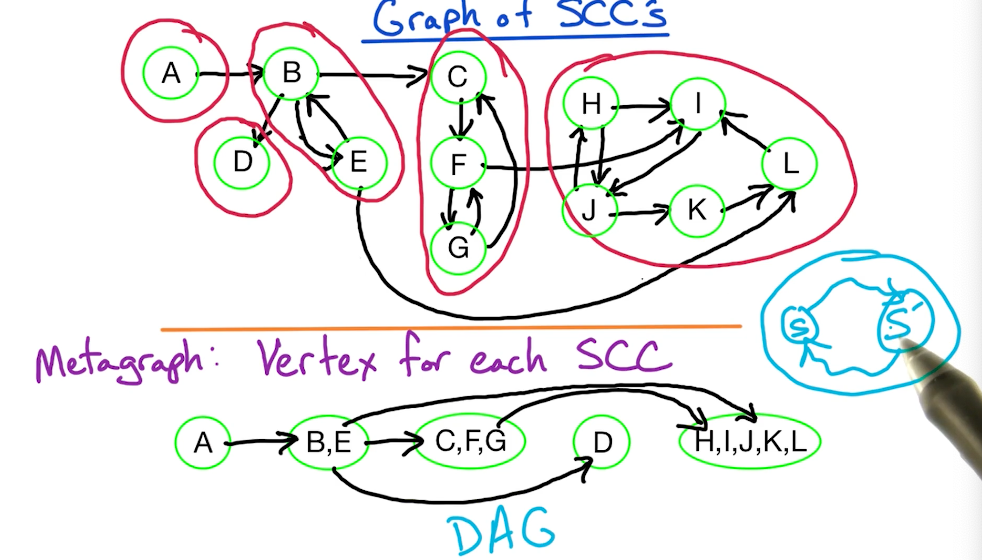
scc-metagraph.png

Tip: The metagraph of SCCs is always a DAG without any cycles. This is always the case since if there is a cycle, then it strongly connects two SCCs which invalidates the fundamental definition of an SCC.

Tip: vertex with lowest post order number does NOT always lie in a sink SCC. However, vertex with highest post order number always lies in the source SCC.

Since we are looking for a vertex in sink SCC, we can utilize the above fact to our advantage

  • reverse the edges of the graph,
  • Run DFS and get post order numbers
  • The vertex with highest post order number lies in the source SCC of this reversed graph, which is the sink SCC of the original graph.

scc-algorithm.png

# Floyd-Warshall Algorithm

Video Demo

# Minimum Spanning Tree (MST)

# Input

The input to the MST problem is an undirected graph with weights for .

# Goal

The goal is to find minimal size connected subgraph. In other words, a spanning tree of minimum weight that connects all the vertices of the graph.

# Properties of Tree

A tree is a connected acyclic graph.

Basic properties of a tree are:

  • Tree on n vertices has n-1 edges. (Because if you have more than this edges there will be a cycle somewhere)
  • There is exactly one path between every pair of vertices
  • Any connected with is a tree

More Properties

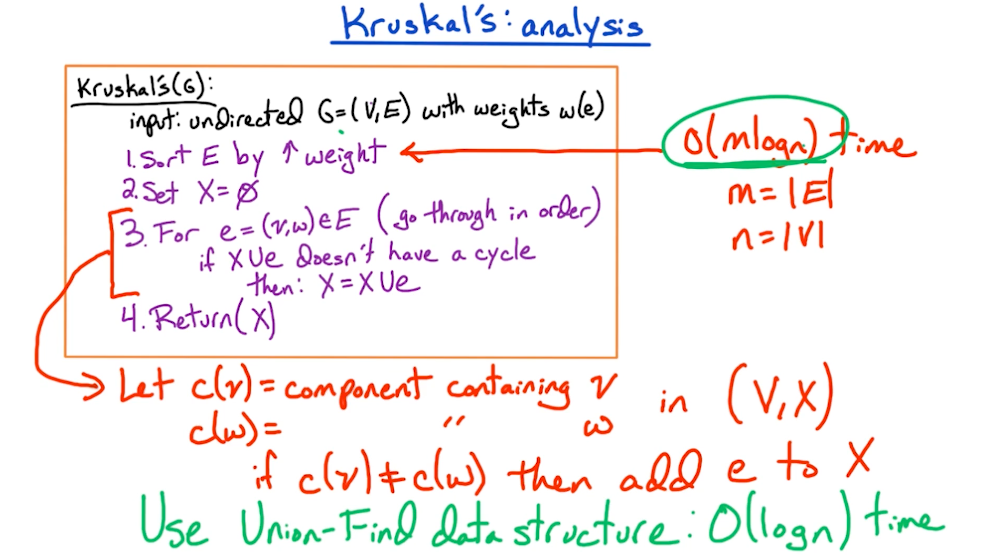
# Kruskal's Algorithm

kruskals-algo.png

# Cut Property

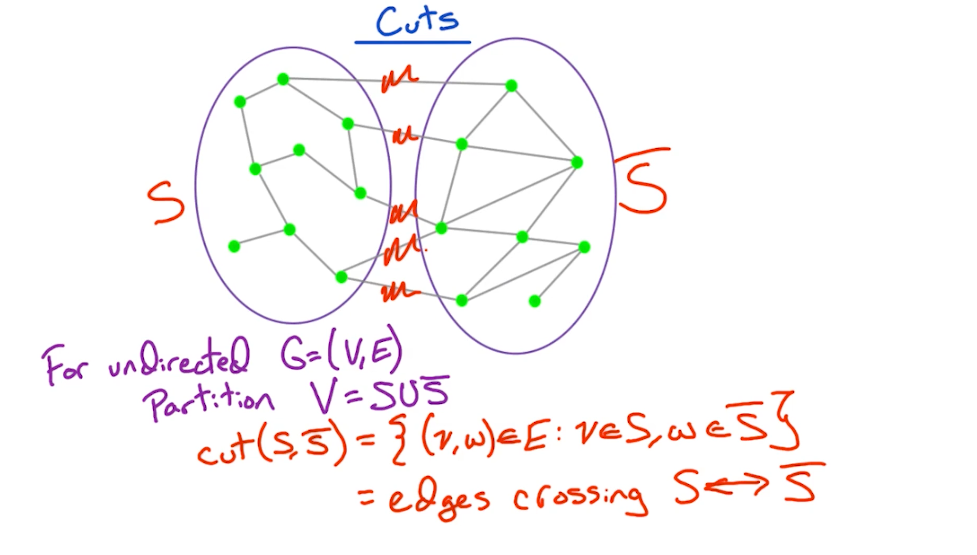
cuts.png

Cut Property: For any cut C of the graph, if the weight of an edge E in the cut-set of C is strictly smaller than the weights of all other edges of the cut-set of C, then this edge belongs to all the MSTs of the graph.

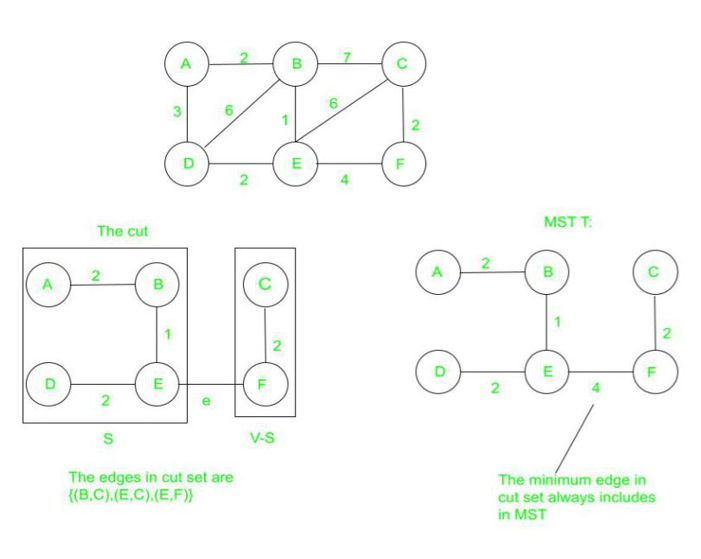
cut-property.png

If all edges are of equal weights, we can find MST in linear time

# Prim's Algorithm

Link

← Satisfiability →