Useful Links | Viveckh's Notepad

# Useful Links

# Overview

Intractable - unlikely to be solved efficiently

Efficiently - we can solve it in times polynomial in the input size

How we do show that a problem is intractable? By showing it is NP-Complete. But we want to be able to say - it definitely cannot be solved efficiently.

# Complexity Classes

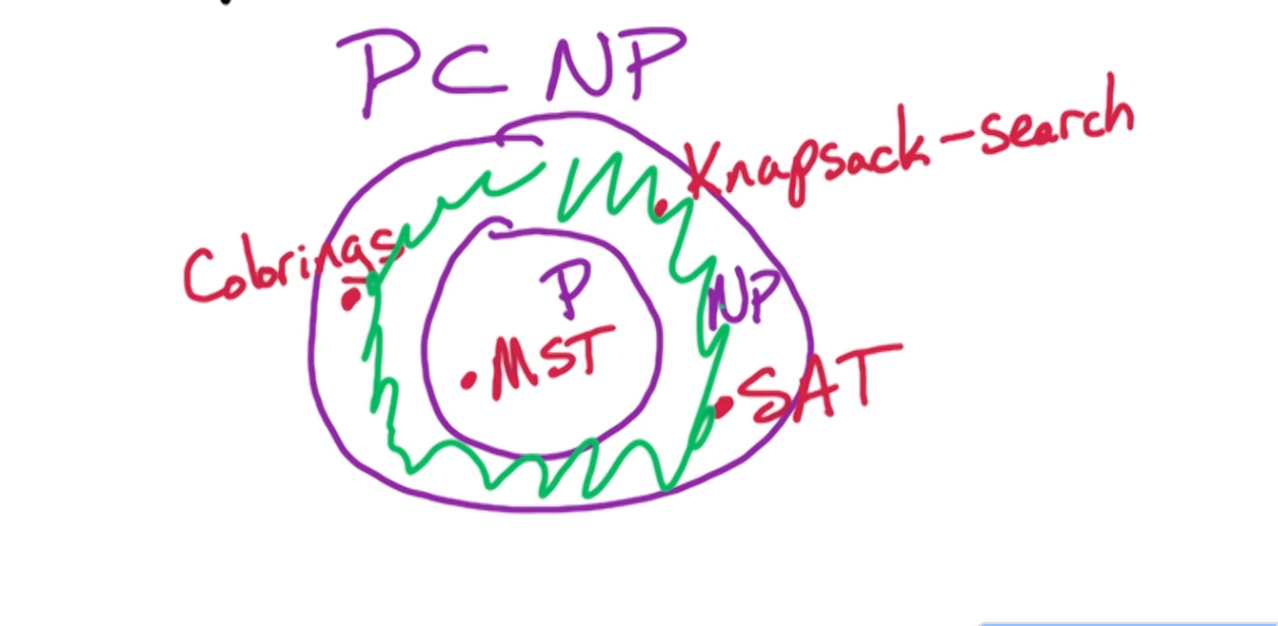
NP = class of all search problems

Search problem in NP: Problem where we can efficiently verify solutions. The time it takes to generate the solution isn't important here, what's important is given the input and the solution, we can verify the solution in polynomial time.

P = class of search problems that are solvable in polynomial time.

Search problem in P: Problem where we can efficiently generate solutions in polynomial time. If we can solve it in polynomial time, we can also verify it in polynomial time, which makes P the subset of NP.

However, it is possible that problems that lie in NP might lie in P as well, but we cannot be certain.

# P vs NP

: means if we can verify a solution in polynomial time of input size, we can also solve it in polynomial time.

: means verifying a solution is much easier than generating the solution.

# Search Problems

# Generic Search Problem

# SAT Problem

Given $f$ and assignment of T/F to x1, x2, ...xn, what is the running time to verify the SAT problem? This is the key to showing .

Proof : Given f & assignment to x1, x2,...xn, it takes time to check that a clause is satisfied. This means, it takes O(nm) total time to verify the solution. Since this is in polynomial time of the input, we can conclude that SAT belongs to NP class of problems.

# Colorings Problem

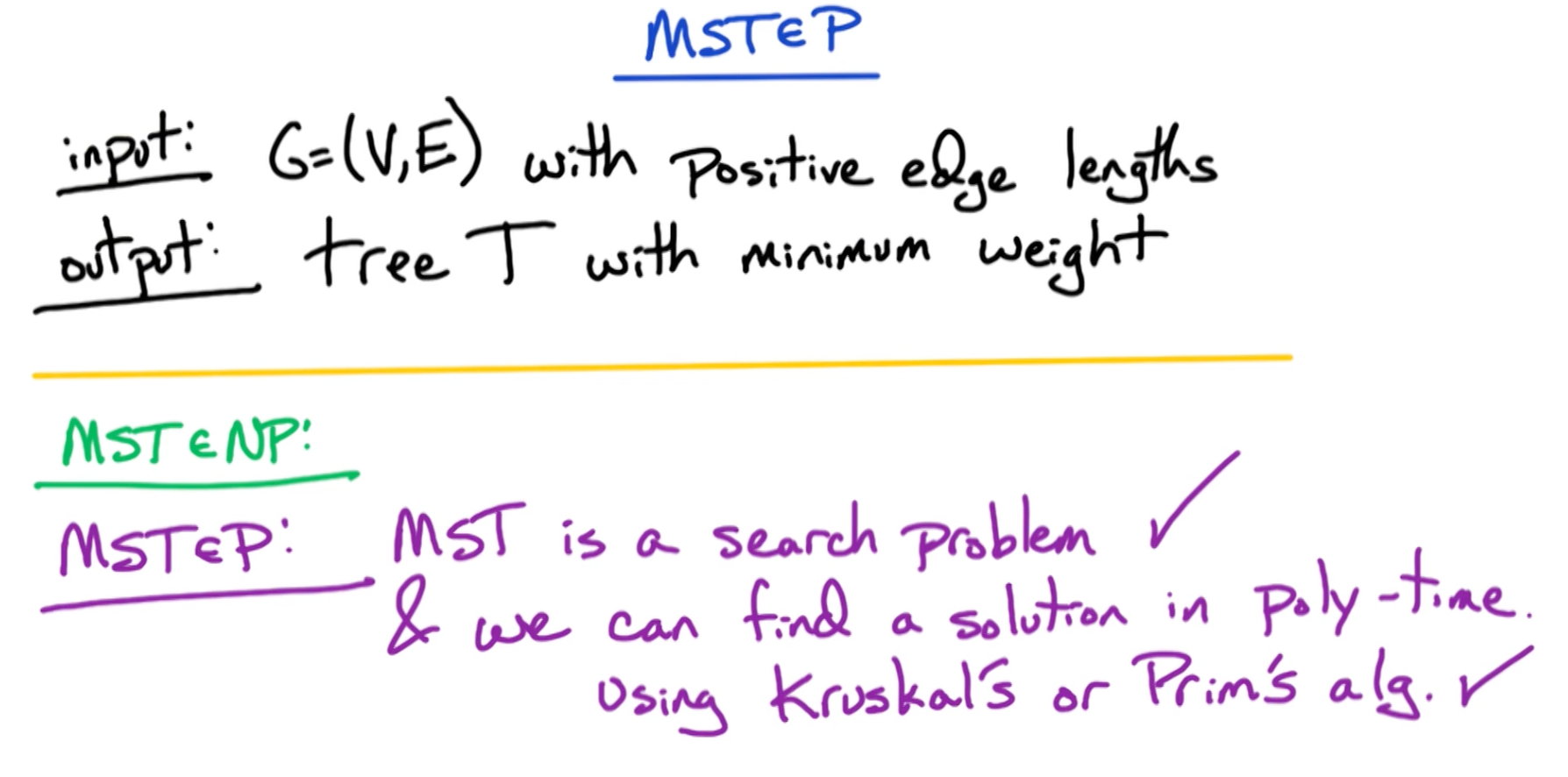
# MST

Kruskal's or Prim's might not generate the exact tree as T, but it is guaranteed to generate a tree of minimum weight. And we just need to compare the weight of that tree is equal to the weight of T to ensure T is MST since we have already shown T is a tree.

To show , we show that MST is a search problem (i.e. ) and then we show that it is solvable in poly-time.

# Knapsack

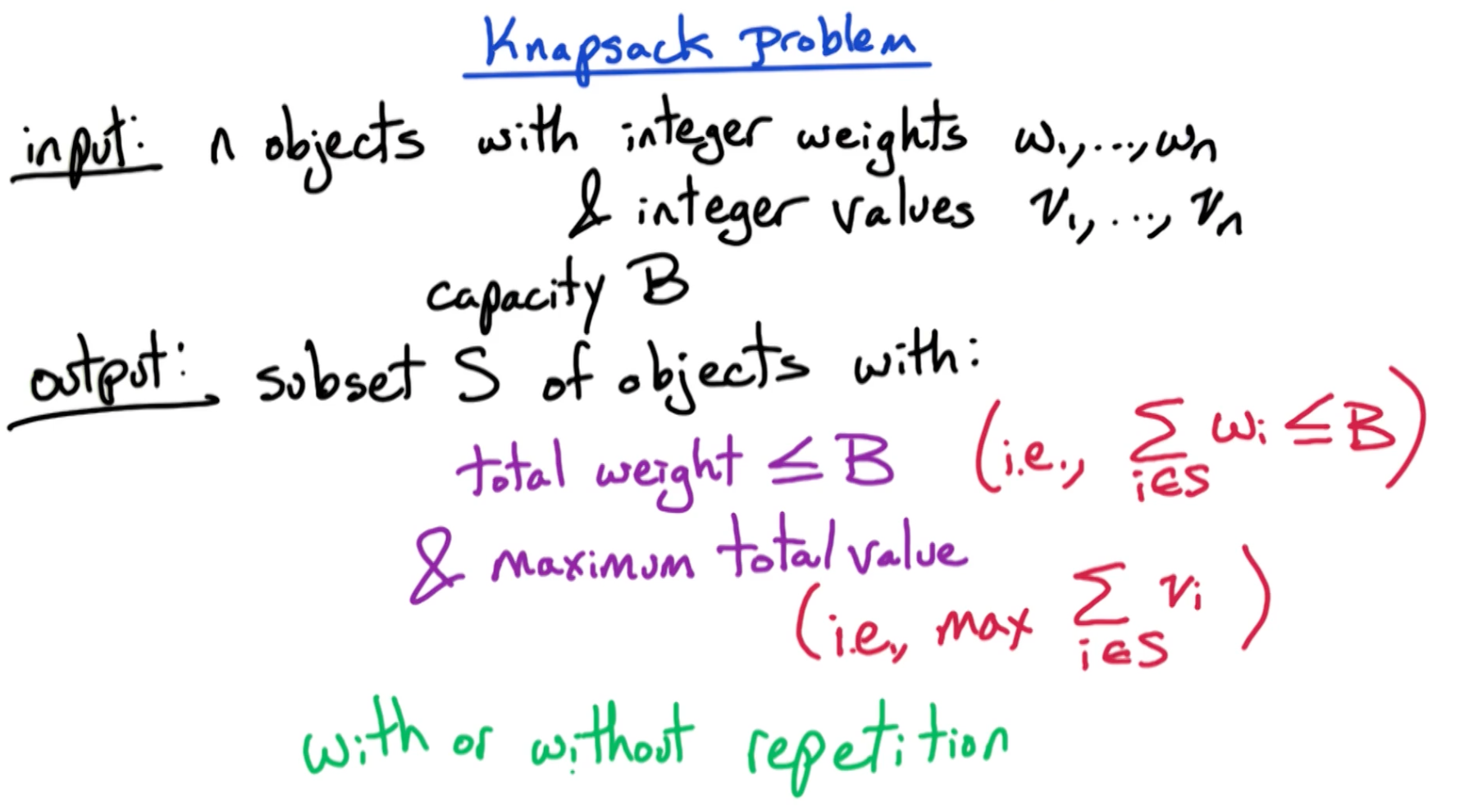
At the moment, we cannot verify in polynomial time whether the solution S has the maximum sum of value possible by staying under the weight B.

However, we cannot confidently state that there is no polynomial time algorithm to verify the knapsack solution, as there might exist one we haven't uncovered. Therefore, it is neither in NP nor not in NP.

Knapsack is not known to be in NP.

And the same logic applies for since the runtime of solving Knapsack is O(nB) which is not poly-time.

# Knapsack Search

Here we are not verifying the sum of values in S is maximum possible sum for given weight total B, but instead that it is at least g. This can be verified in polynomial time by summing up the values in the output S and checking with g.

# Reductions

# Definition

Given problems A & B, or means reducing A to B or B is at least as hard as A.

This means, if we can solve problem B in poly-time, we can use that algorithm to solve A in poly-time.

# How to reduce

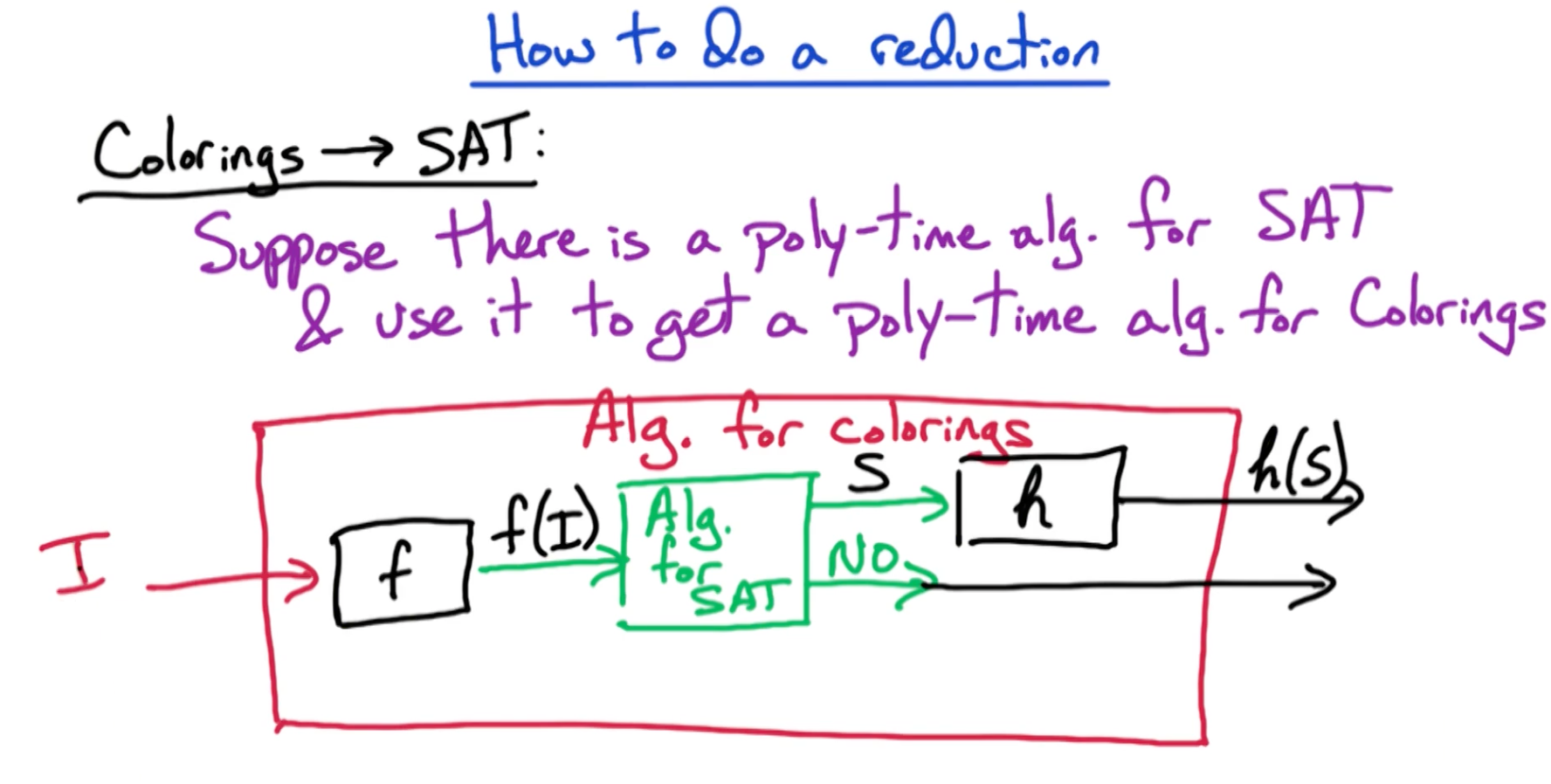
$f$ takes the input for colorings aka I and transforms it to input for SAT aka
$h$ takes the solution for aka $S$ and transforms it into solution for colorings
We need to prove that: $S$ is a solution to is a solution to $I$

# NP-Completeness

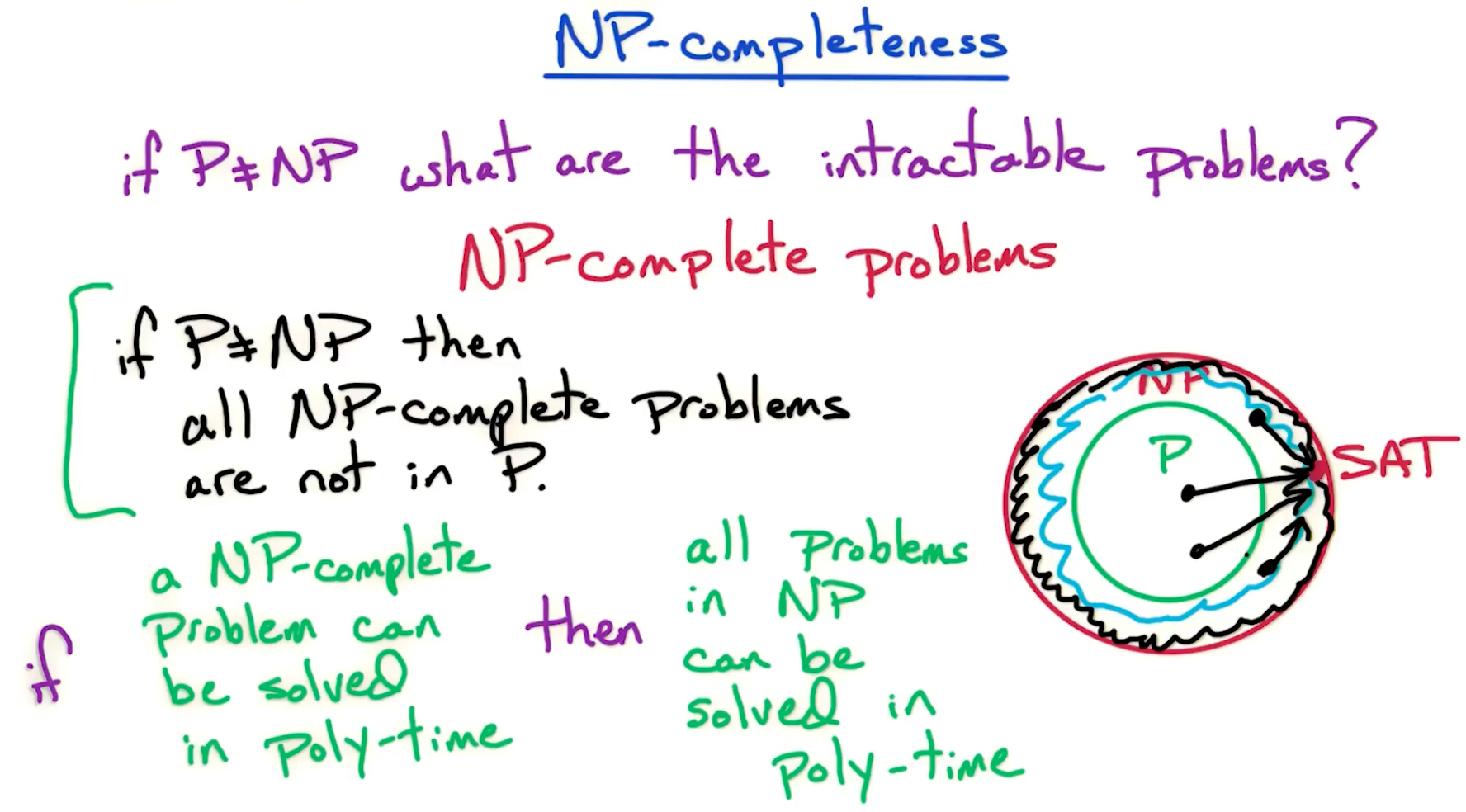
There are some problems that lie in the donut region, outside P in the non-overlapping region. These problems are NP-Complete problems.
NP-Complete problems are the hardest in the NP class of problems.
If , then all NP-complete problems are not in P.
Alternatively, this can be stated as - If there exists an NP-complete problem that can be solved in poly-time (i.e. it is in P), then, all problems in NP can be solved in poly-time.
Hence for a problem such as SAT that lies in the NP-complete portion of the donut, we have to show that if there is a poly-time algorithm for solving SAT, then there is a poly-time algorithm for solving all problems in the class NP. We just have to use SAT's poly-time as a black box, and reduce every NP problem to SAT which allows us to solve the problem in poly-time.

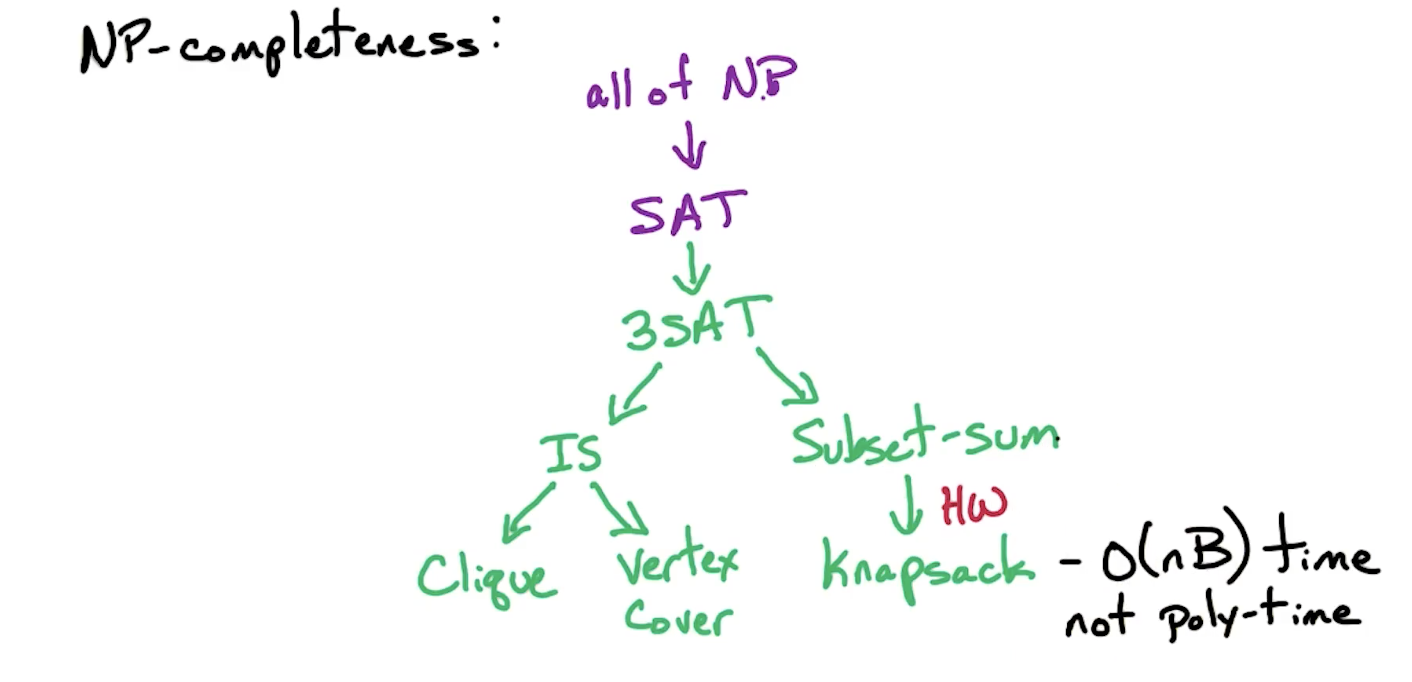
# If SAT is np-complete

The second requirement means SAT has to be the hardest problem in the class. For SAT to be hardest in the class, it means it is the least likely to have an efficient solution. This means, if we have an efficient solution for SAT, then we can solve every other problem in NP in polynomial time i.e. NP = P.

However, at the moment, this is no polynomial-time algorithm for SAT. If they did, we would have been able to prove P = NP.

# How to prove

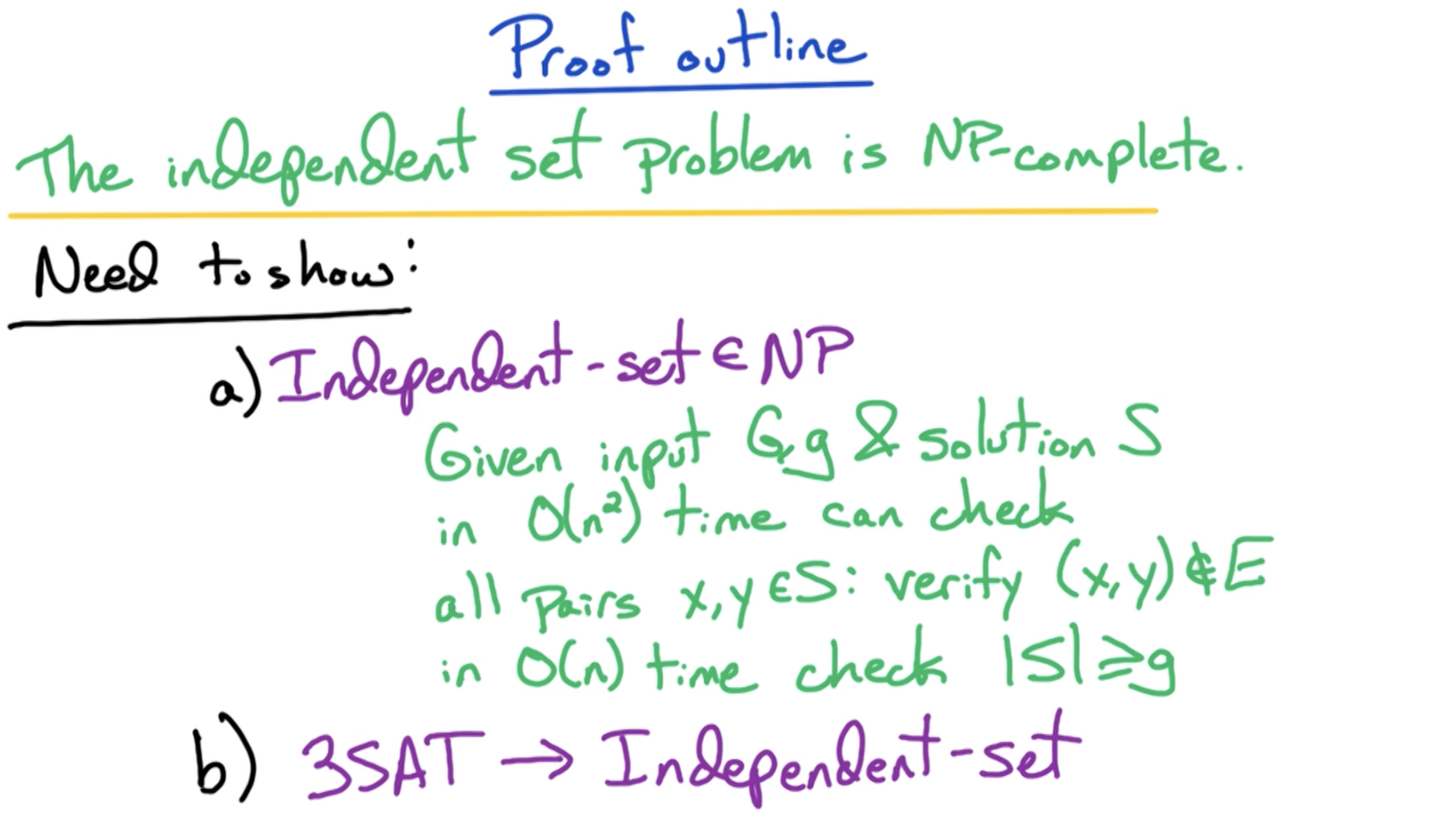
To show, Independent Sets (IS) is NP-complete, we need to show:

for all ,
- To show this second part, we need to start with a known NP-complete problem.
- Suppose we know SAT is NP-complete, then, we show i.e. the SAT problem can be reduced to IS.
- Then since , it means which means

# SAT -> 3 SAT

Skim through NP2 Lectures to revisit the concept before exam.

Also outlined in Joves notes.

For the general approach and layout of solving similar problems, look at HW7 solution. It expresses my understanding in an intuitive manner.

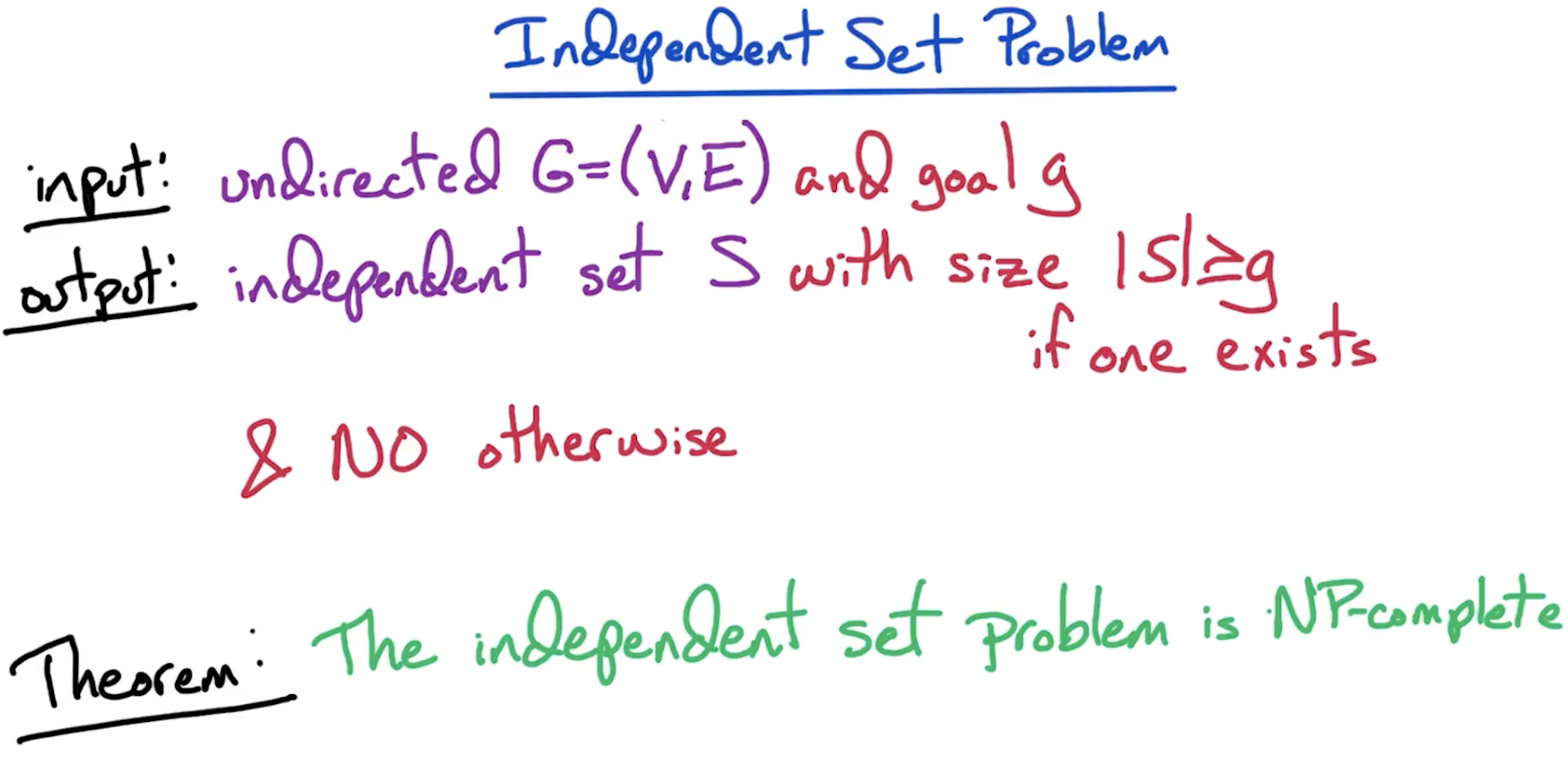
# Independent Set (IS)

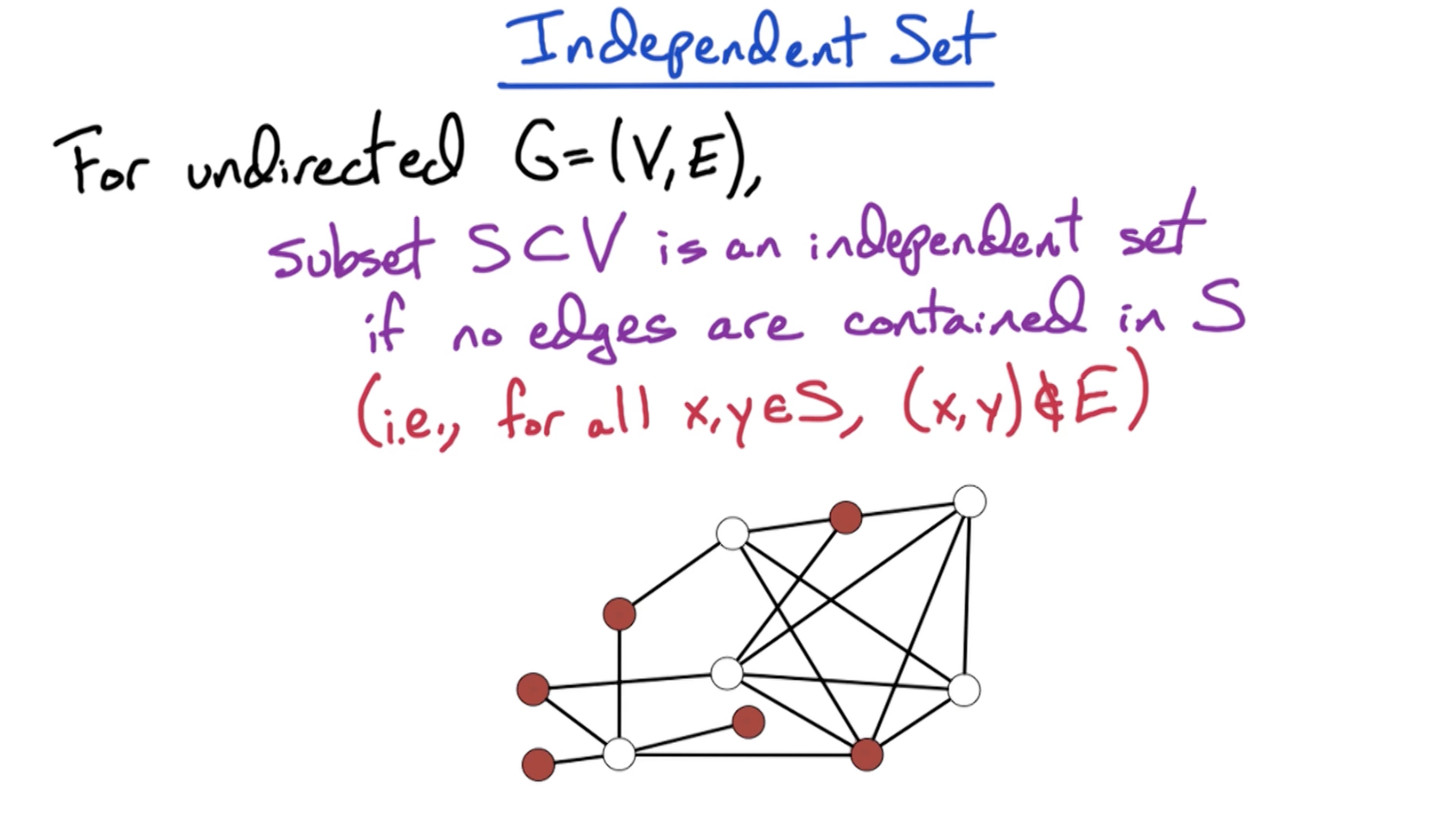
Empty set is an independent set too and so is a single vertex by itself.

The max-independent set is not known to be NP because to verify it in polynomial time, we actually have to solve the whole thing in polynomial time. And to be able to solve it in polynomial time, it needs to be in class P. and if P != NP, then max-independent set cannot be NP.

# Problem

# Proof outline

# 3SAT -> IS

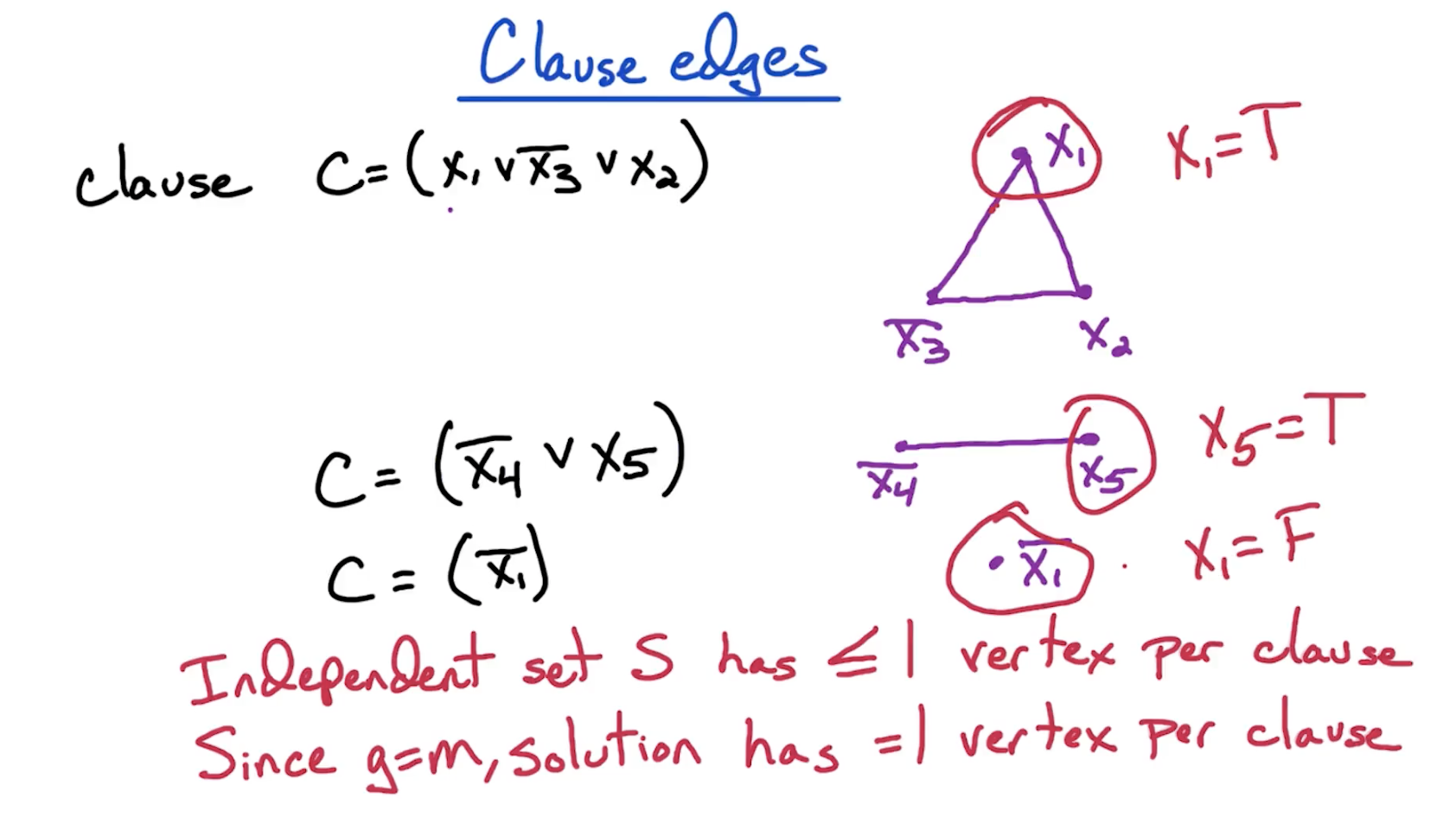
But this alone is not enough since we can accidentally assign x1 two values in two different clauses. This gives rise to the idea of variable edges described below.

We will add edges between all copies of and all . This will ensure that the two clauses with and will get connected and treated as one big clause. And since we are trying to only pick one vertex per clause, we will never end up picking both and .

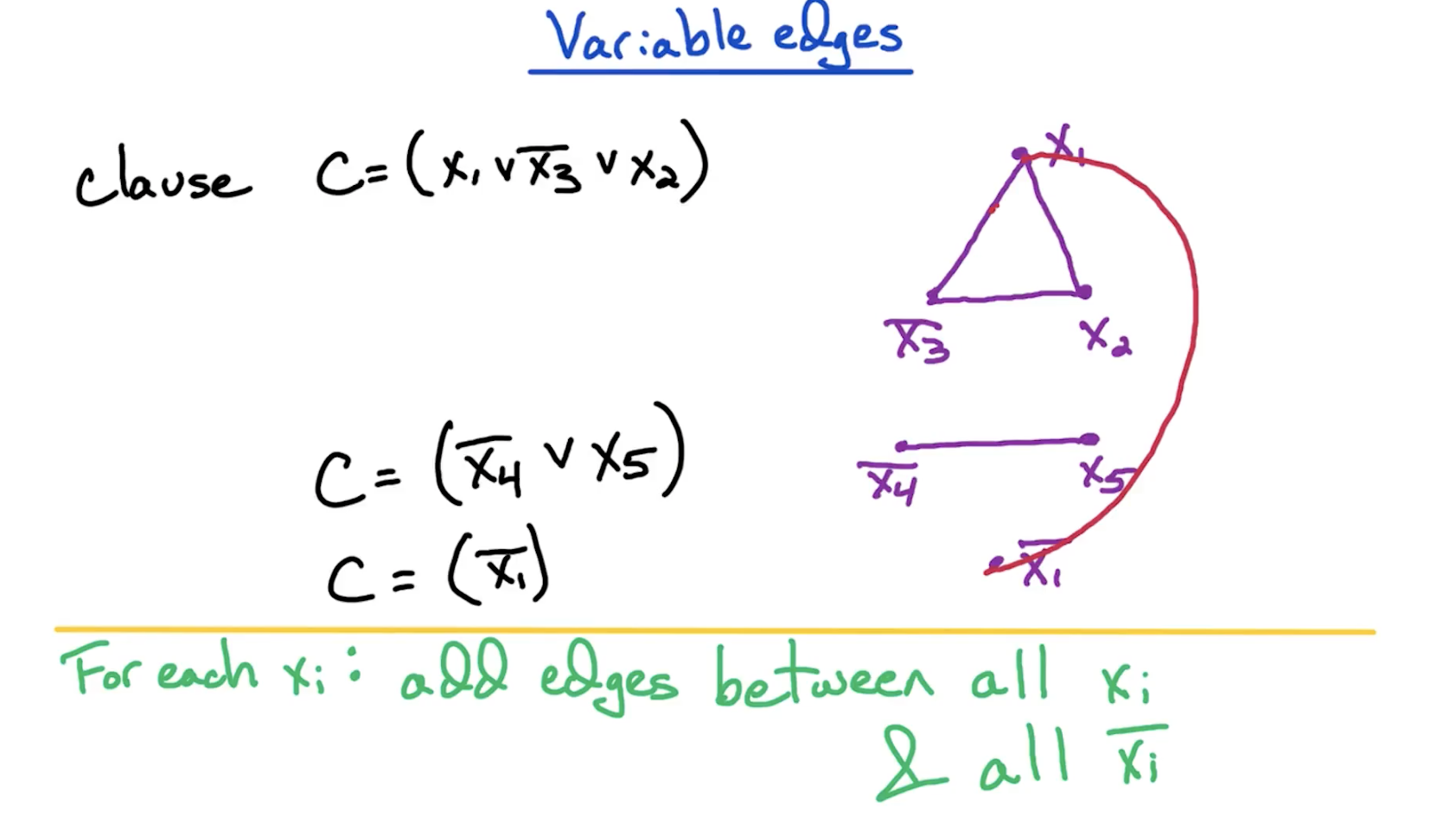
Look at an example below.

We first connect the edges of a single clause.
Then we connect and kind of relationships.
And if we pick one value from each clause to satisfy ensuring no contradiction exist for a IS of size 4, we get the following.

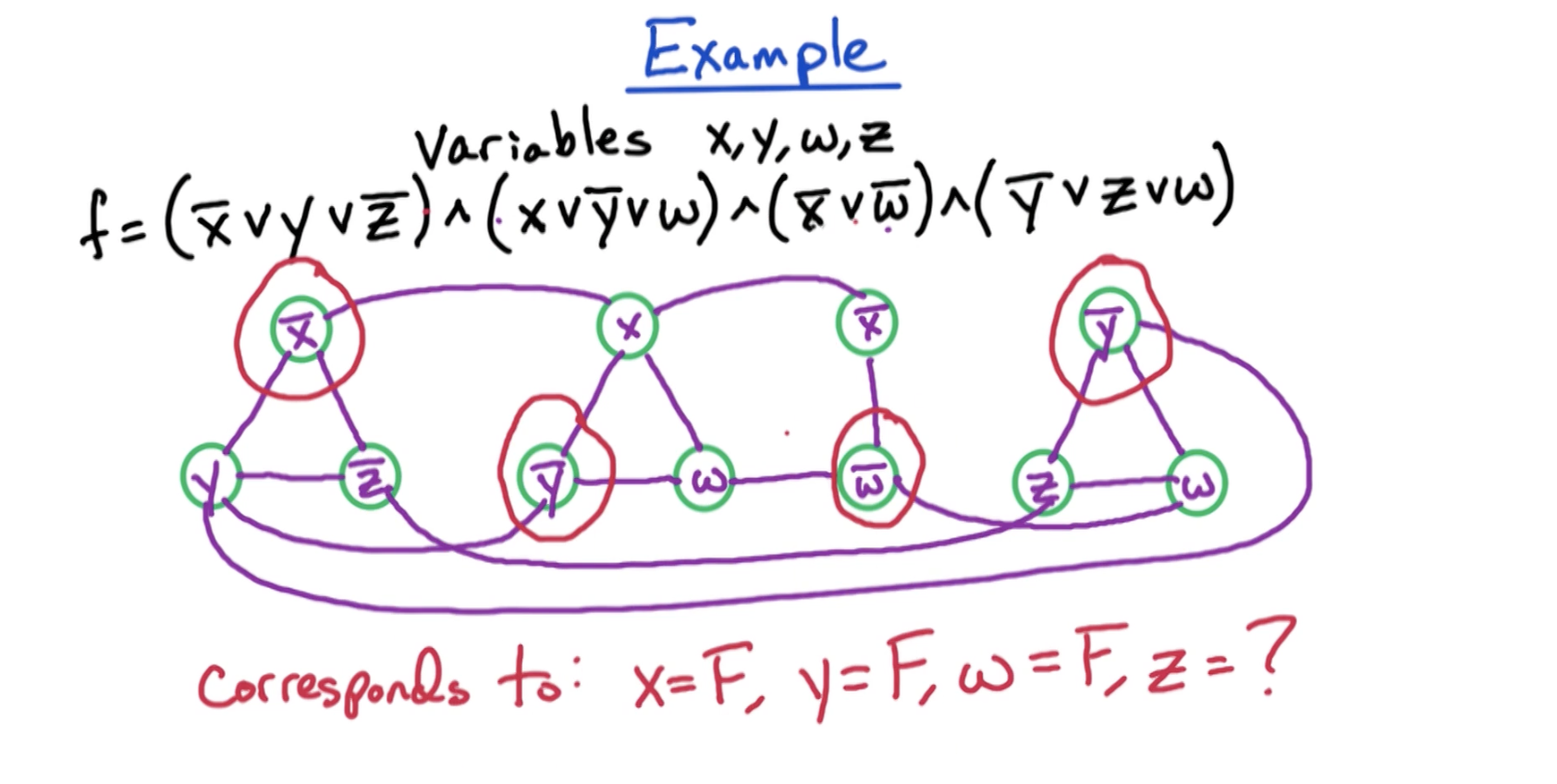
# Correctness

# NP-Hard

IS is NP-complete but Max-IS is NP-Hard.
There is a reduction from every problem in NP-class to IS. It is at least as hard as every problem in this class of NP.
Reducing IS -> MaxIS is straightforward. Which means there is a reduction from every problem in class NP to the MaxIS problem either directly, or by going through IS. This means, Max-IS is at least as hard as every problem in the class NP.
If we can solve Max-IS in polynomial time, we can solve every problem in NP in polynomial time.
NP problems are hardest in the NP set. However, NP-Hard are at least as hard as everything in the NP set.

# Clique

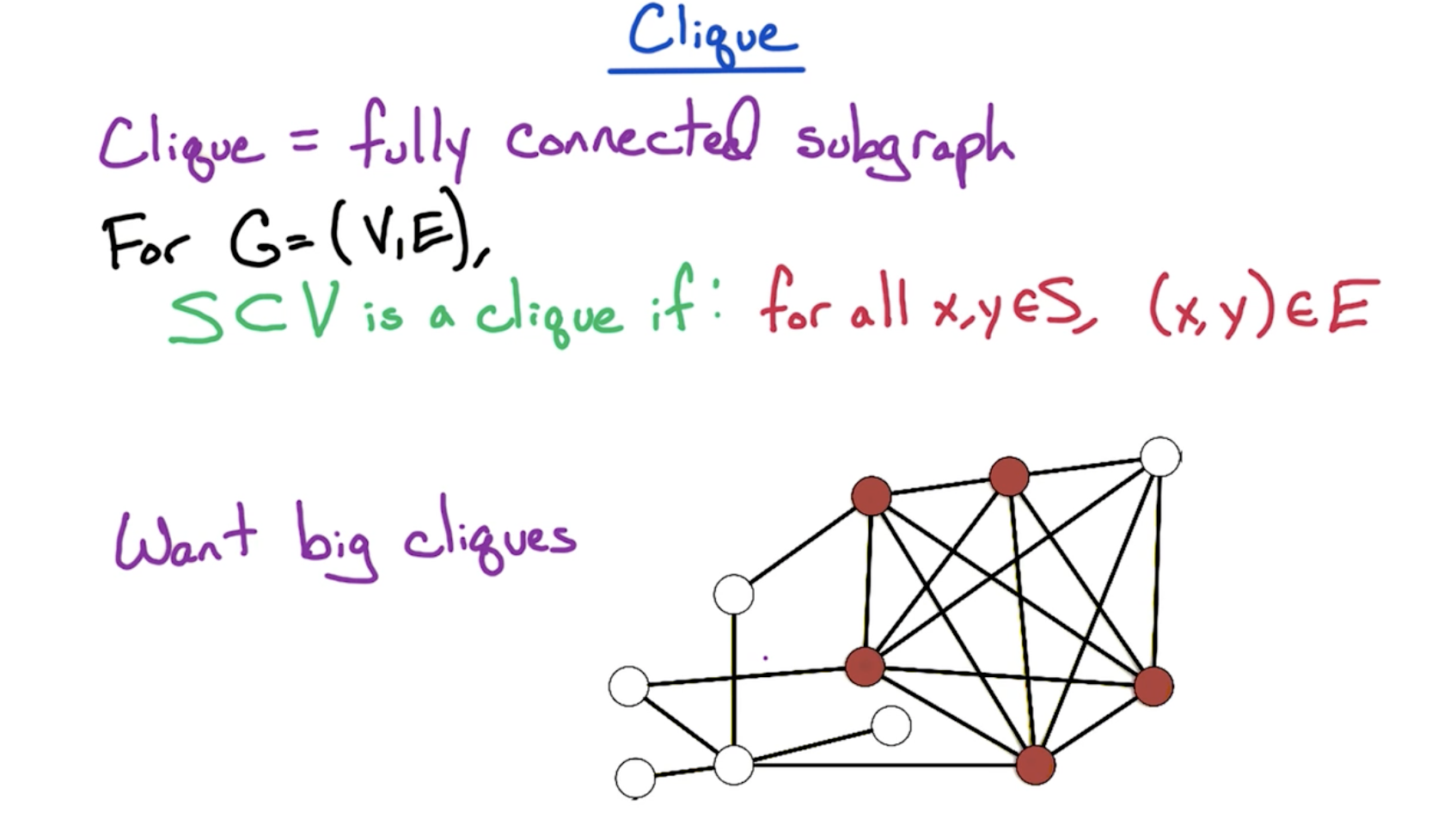
Empty set, single vertex, two connected vertices are all cliques. The challenge is finding bigger cliques.

# Problem

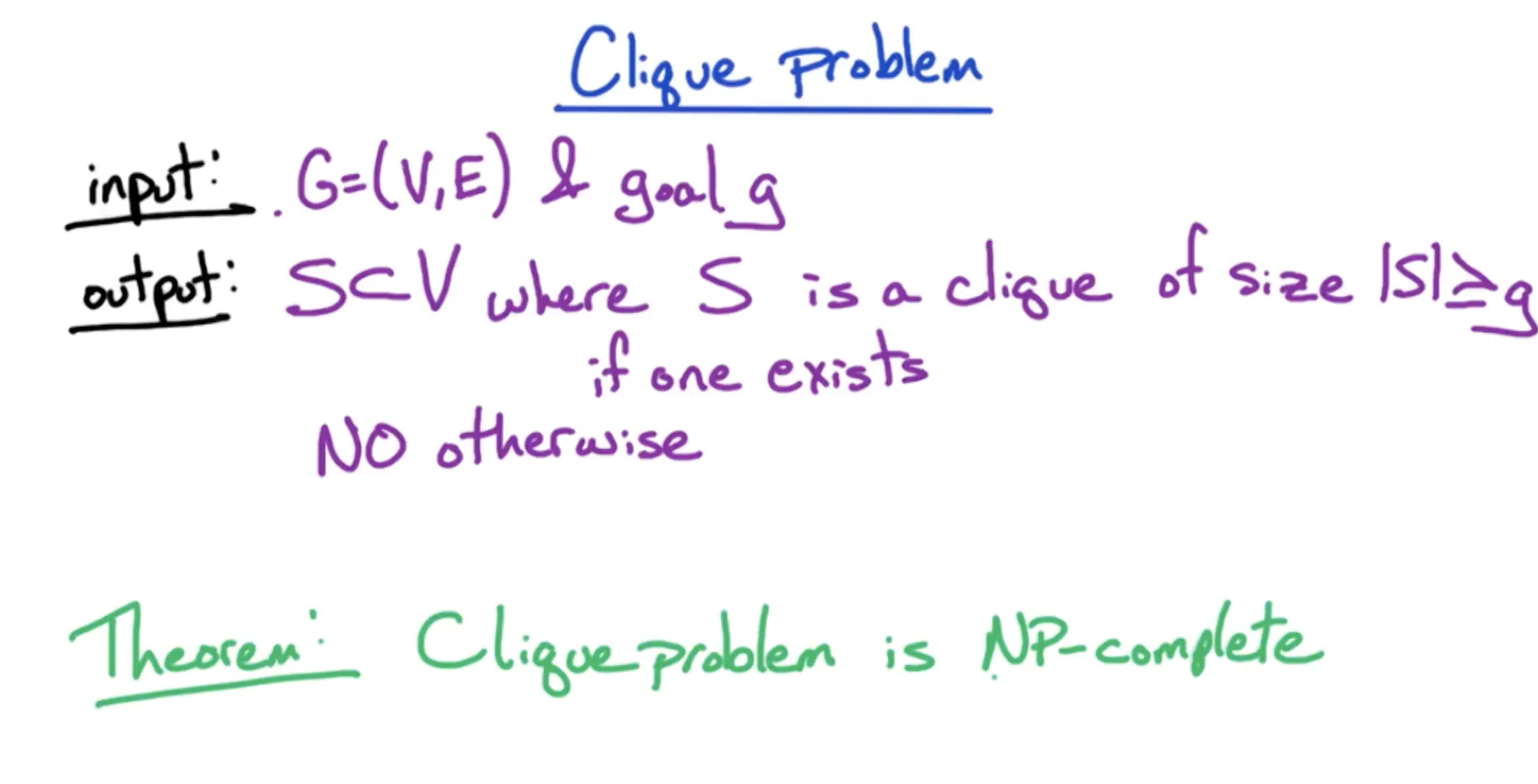
# Proof Outline

# IS -> Clique

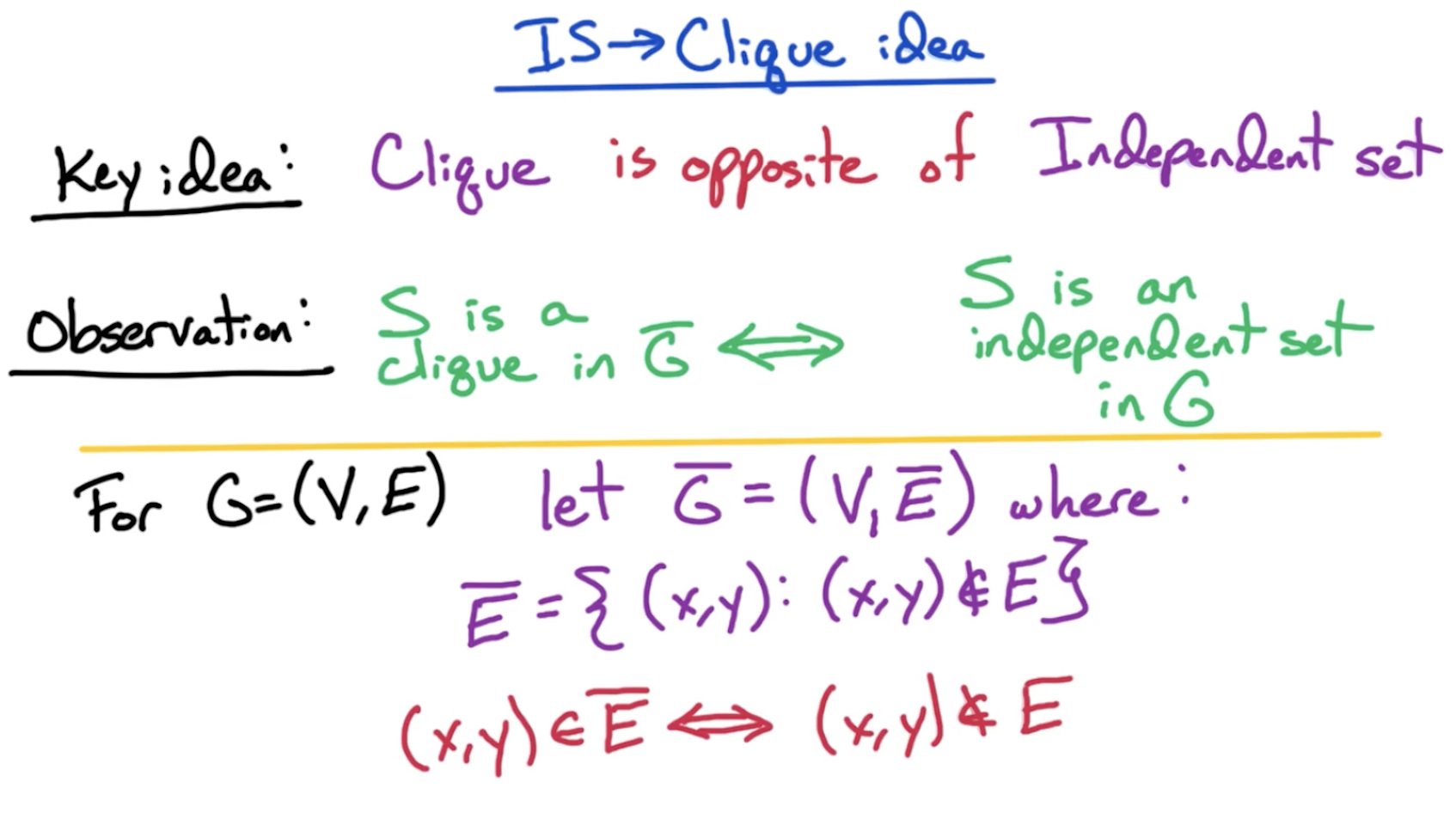
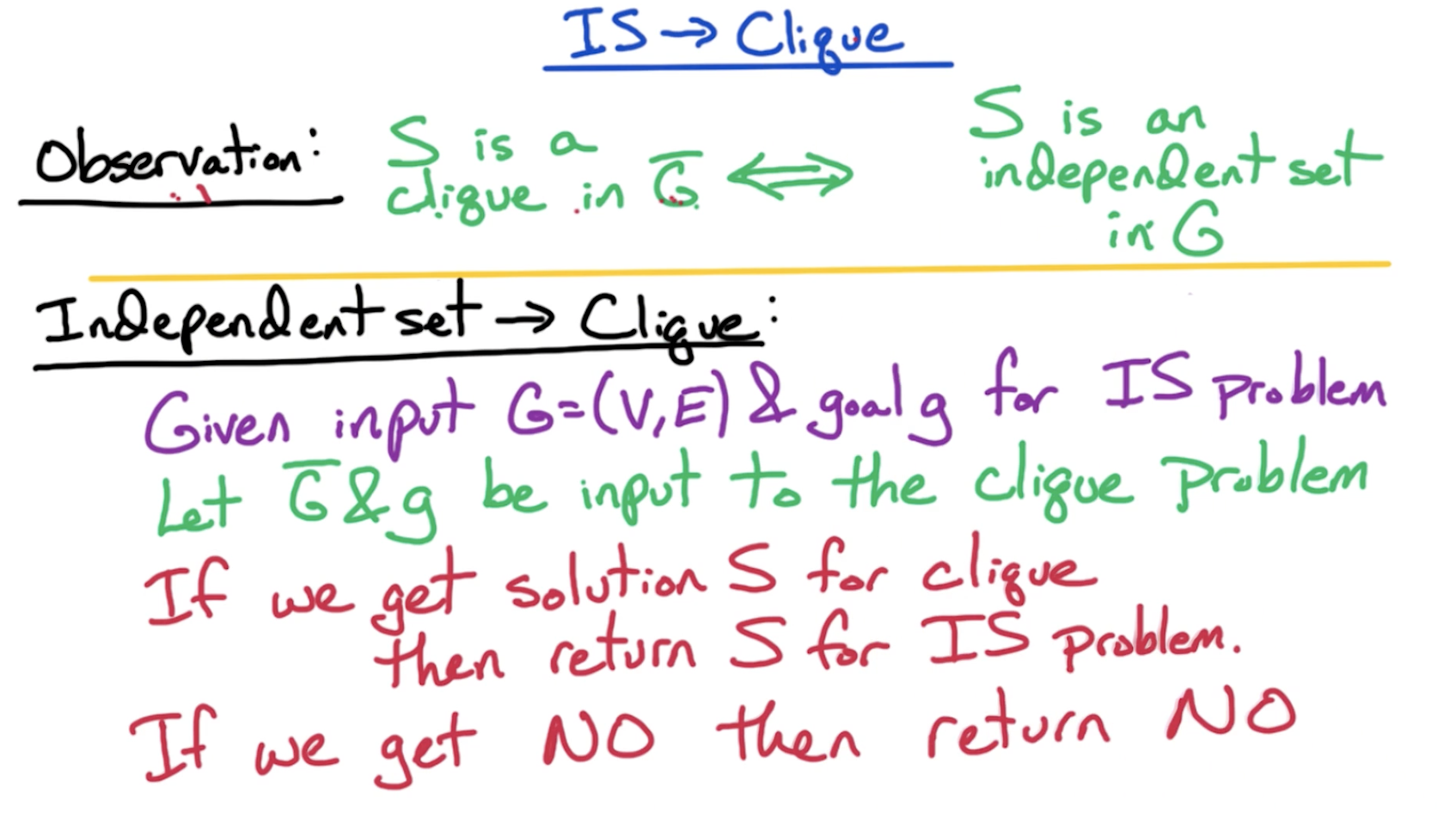
# Vertex Cover

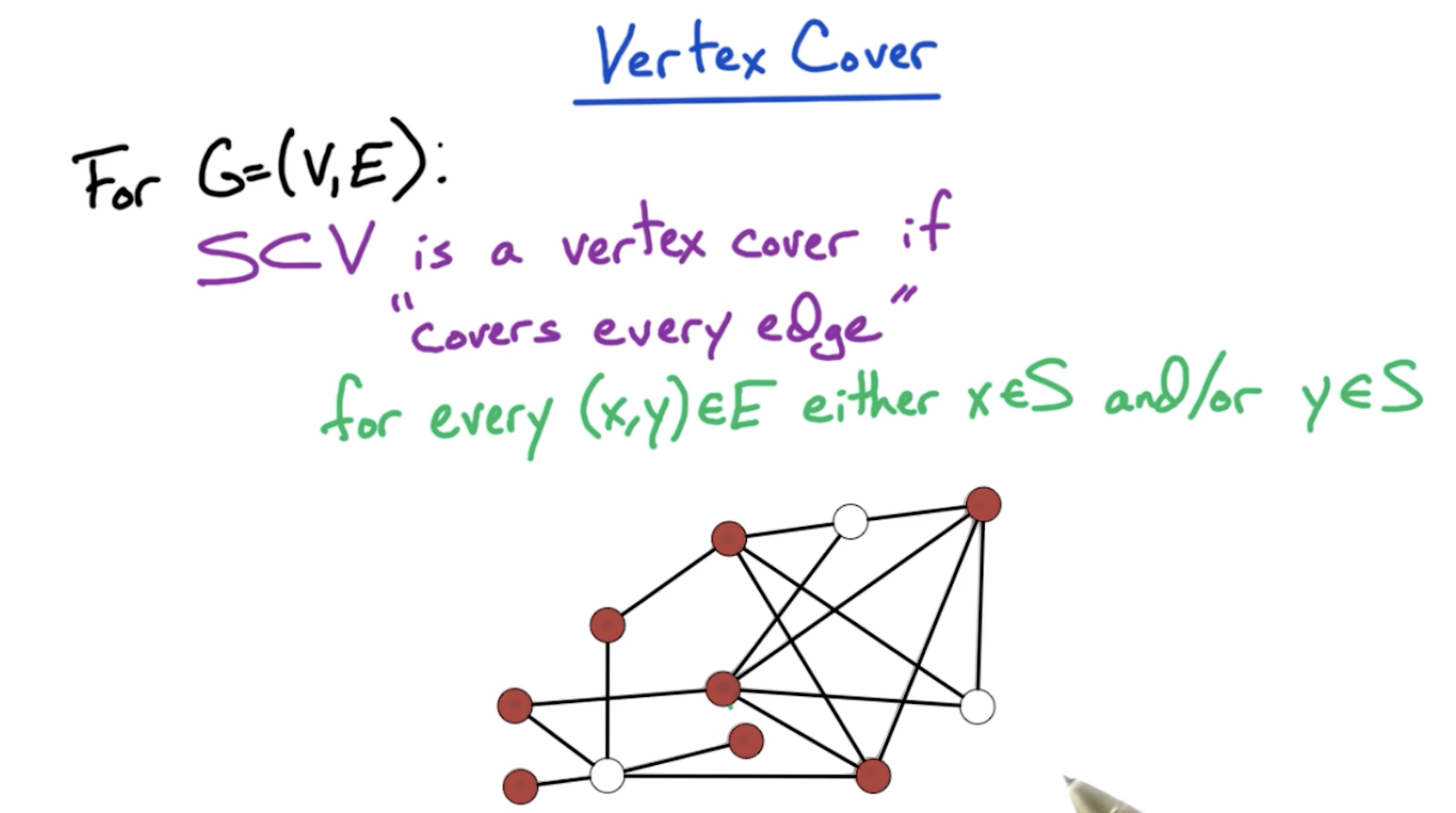
It is trivial to find a large vertex cover since we can include all the vertices of the graph. The challenge is finding the smaller vertex cover.

# Problem

# Proof Outline

# IS -> VC

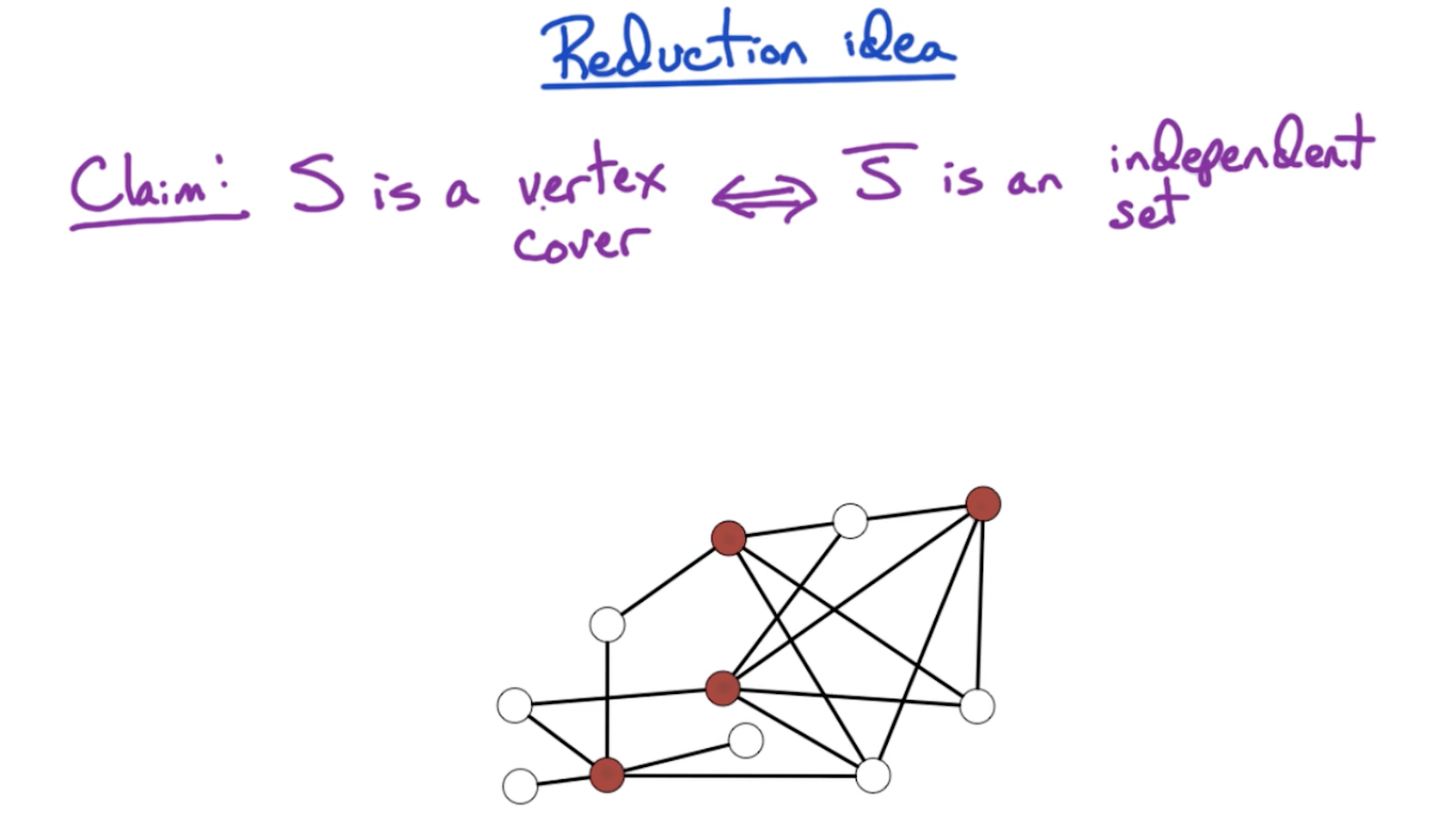
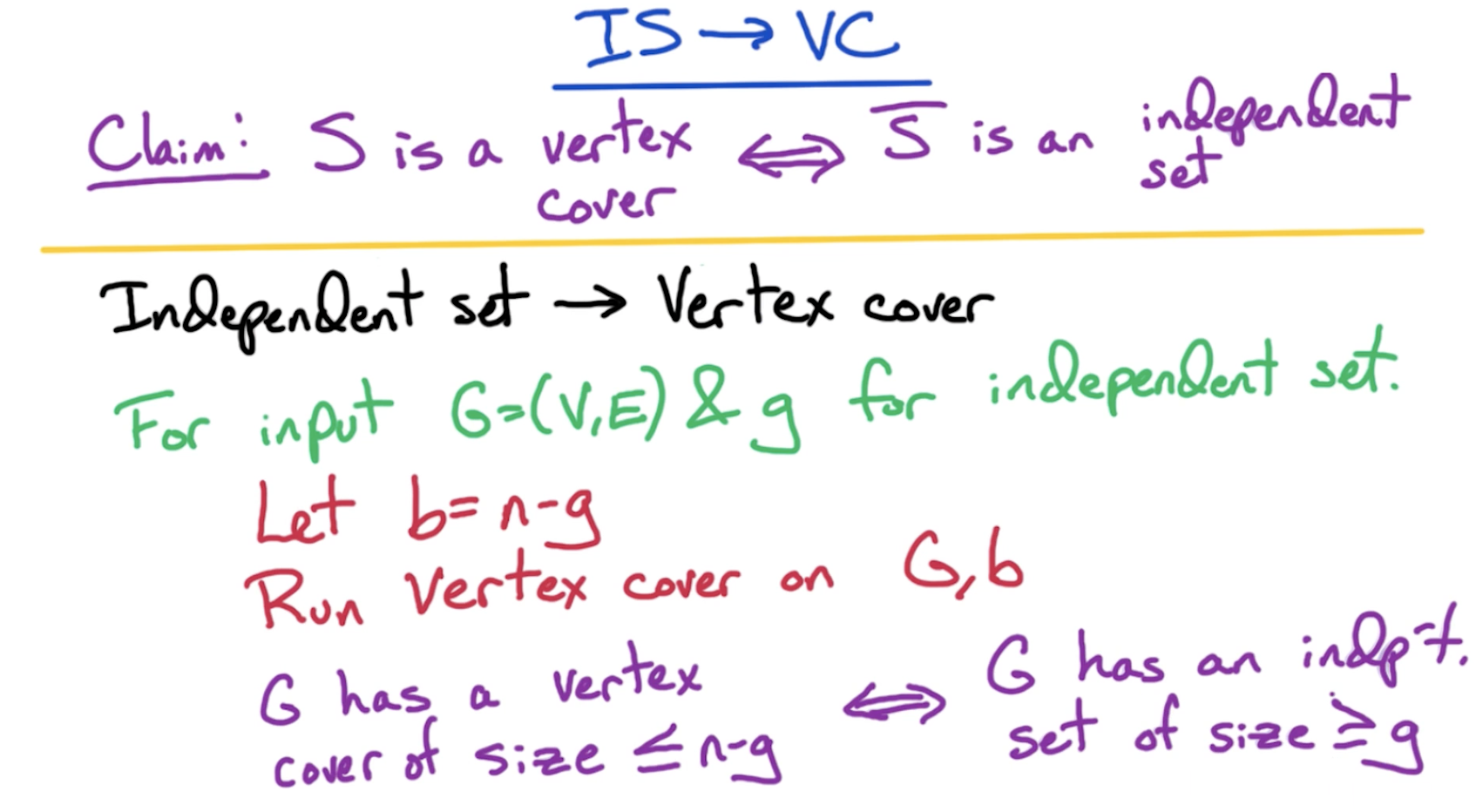
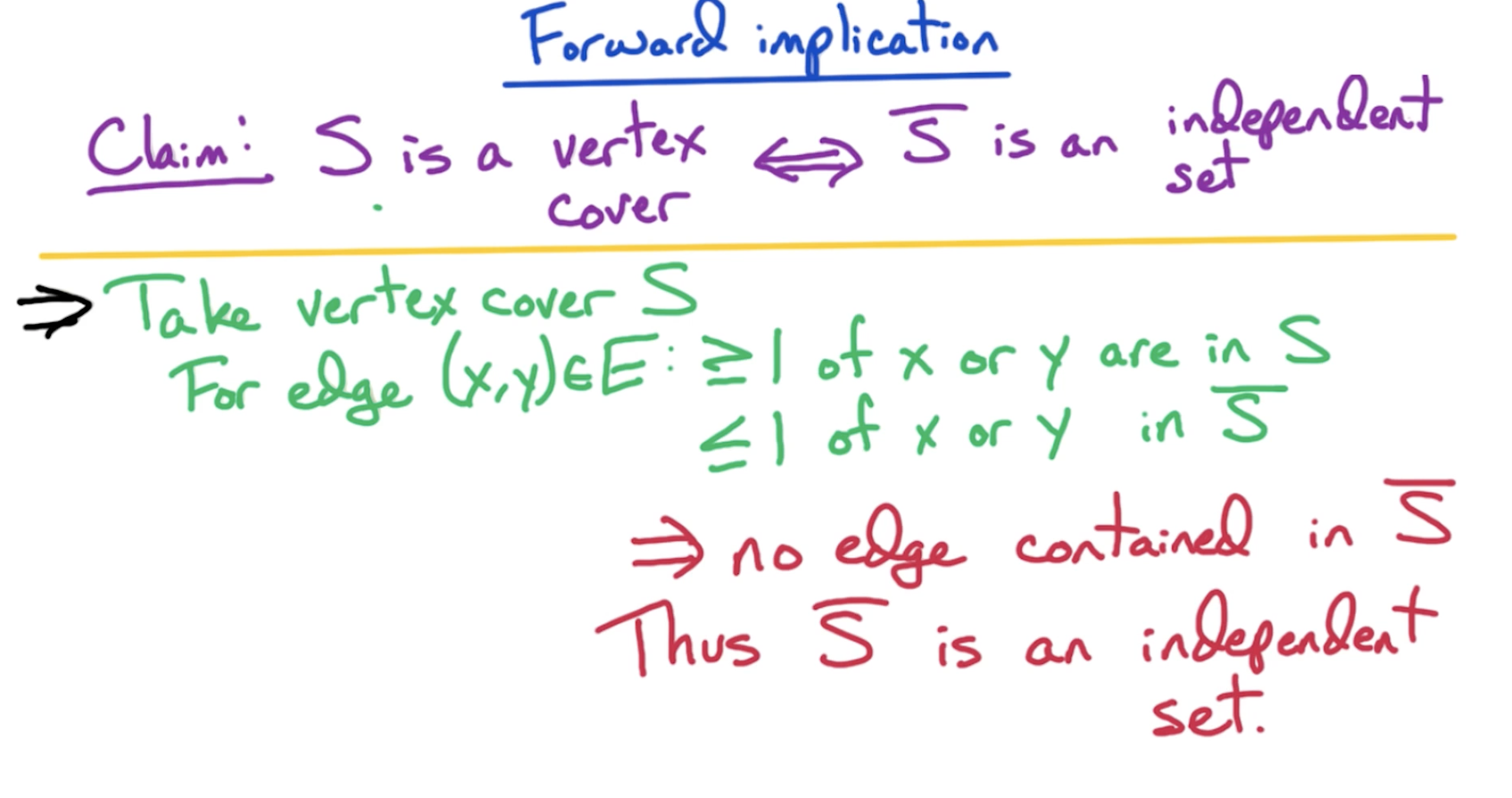
# Correctness

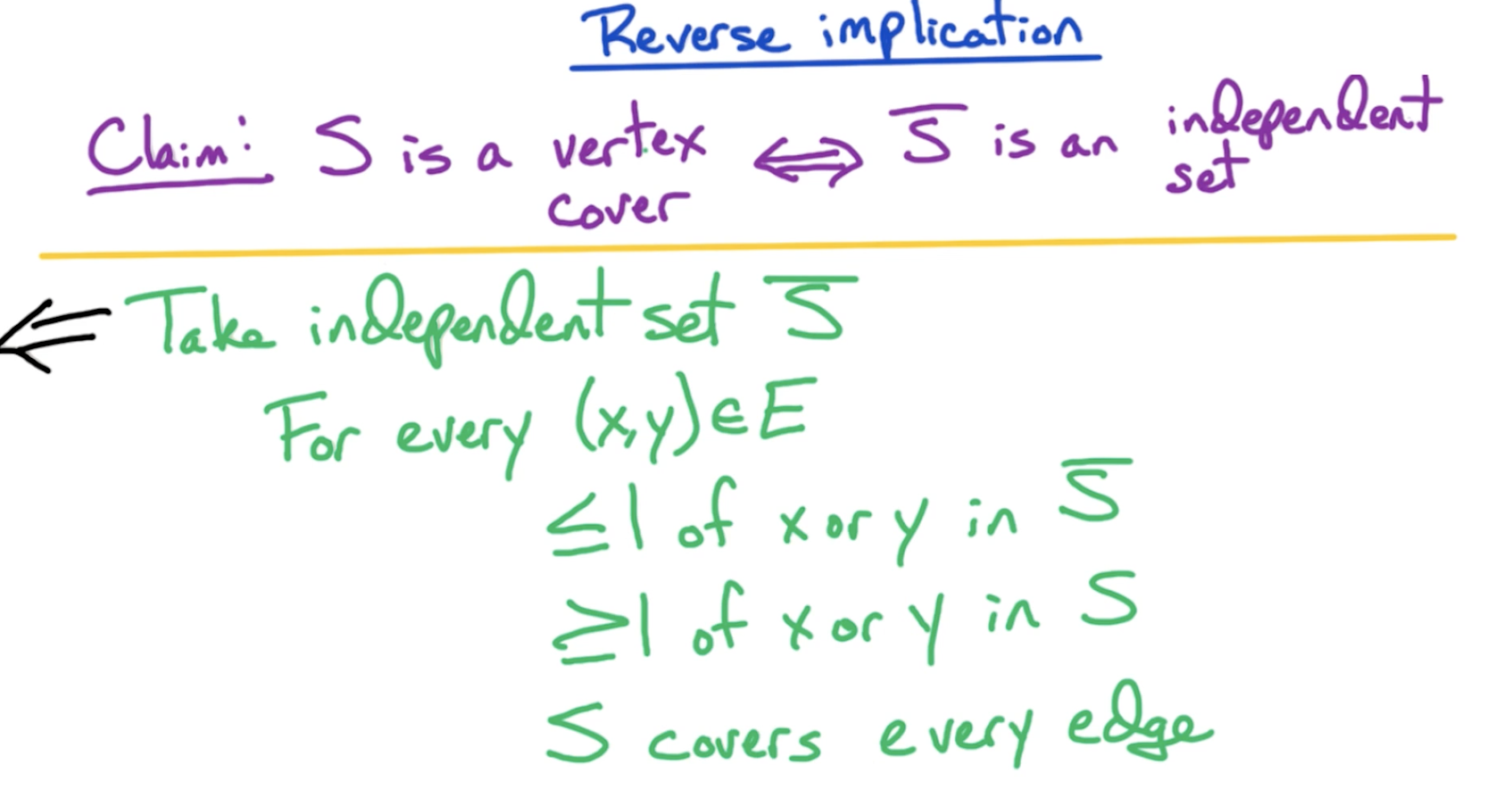
# NP Proof Approaches

Two flavors of NP-Complete problems to show:

Proof by Generalization: showing that the new problem is more general than the known problem. You can just set the parameters in the new problem to get the output for the known problem
Gadget: We take the known problem and modify it or add something to it (like adding vertices to a graph etc) to make it fit the new problem and them solve it.

# Subset Sum

# Proof Outline

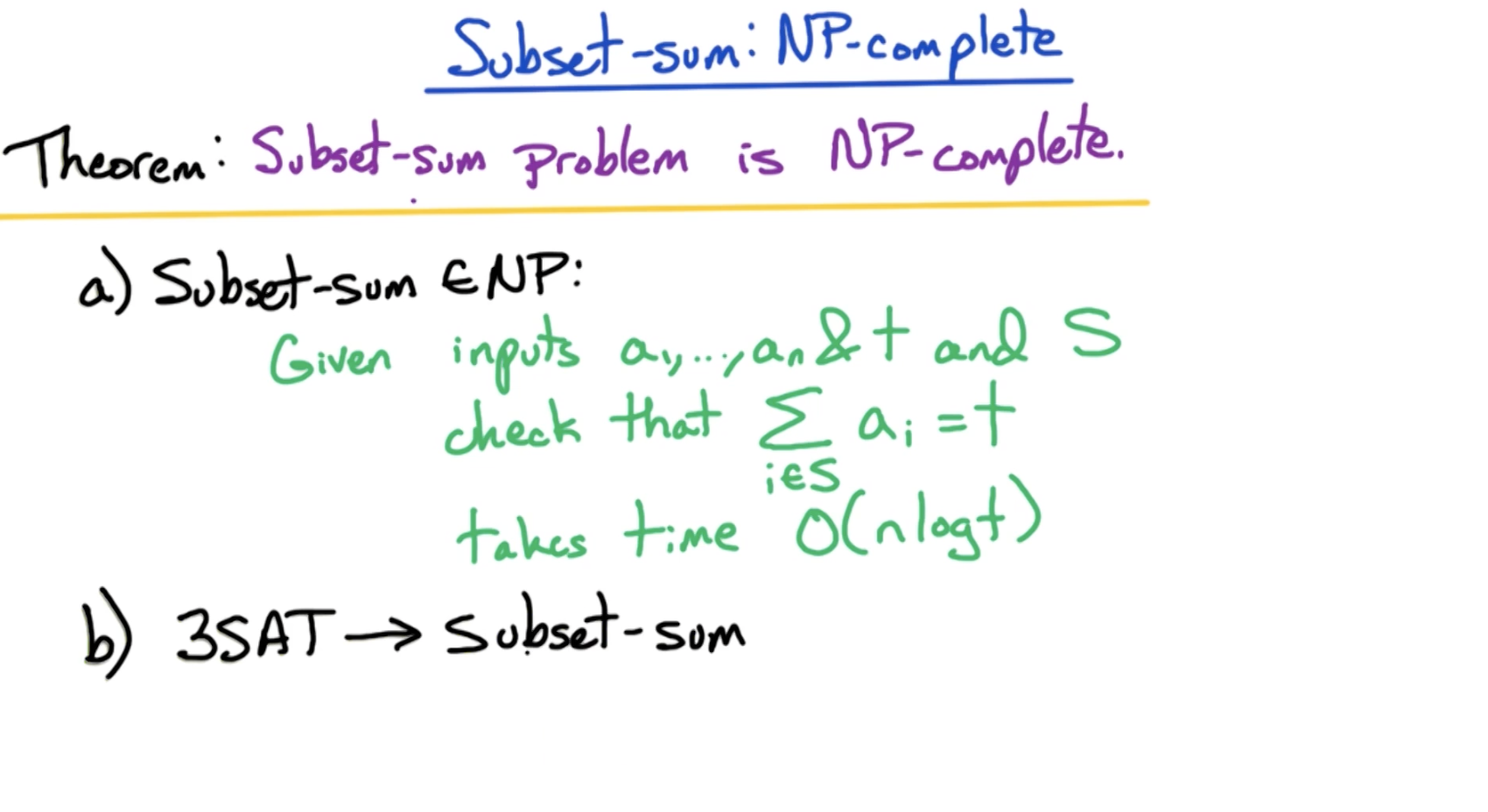
# Counterpositive Logic by Richard

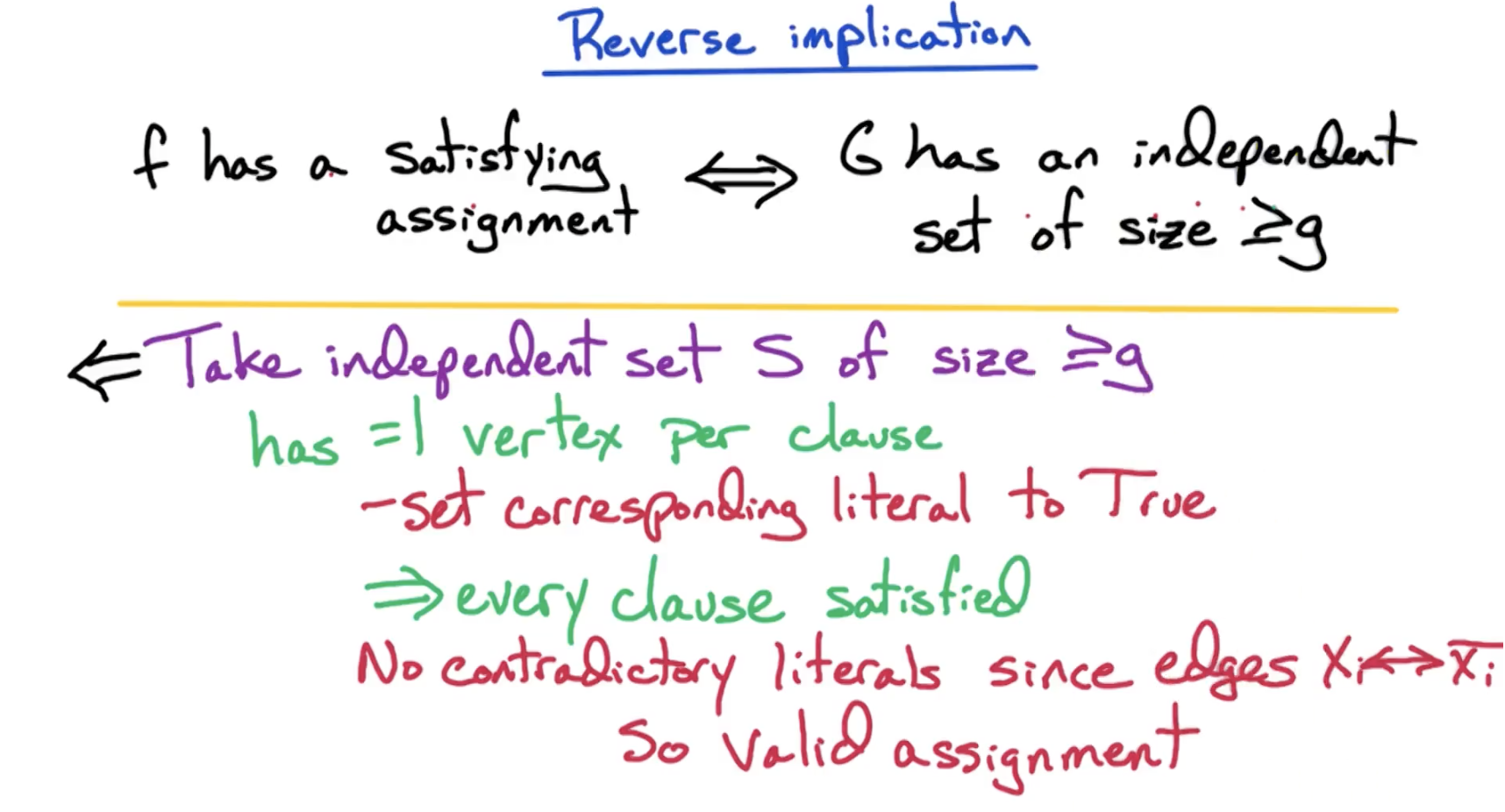
In NP-C we have to prove "A has a solution if and only if B has a solution", so we have to prove our two implications "if A has a solution then B has a solution" AND "if B has a solution then A has a solution".

This is where the contrapositive comes into play. Maybe instead of proving "if B has a solution then A has a solution", it would be easier to prove "if A has NO solution, then B has NO solution". Since these are contrapositives, we can interchange them. If we do this, then we will have to prove our two implications "if A has a solution then B has a solution" AND "if A has NO solution then B has NO solution". Doing this is exactly the same as what we had to prove in the previous paragraph, and doing this will prove "A has a solution if and only if B has a solution"

Below are the four allowed combinations of two implications that will prove "A iff B". You can learn all four and pick the one that is easiest for the problem at hand, you can learn one and stick with it, or anything in between. But these are the ONLY combinations that will work.

To prove "A has a solution if and only if B has a solution" we can prove:

"if A has a solution then B has a solution" AND "if B has a solution then A has a solution"
- this is the standard, "both positive" implications
"if A has a solution then B has a solution" AND "if A has NO solution then B has NO solution"
- this swaps the second positive implication for its contrapositive
"if B has NO solution then A has NO solution" AND "if B has a solution then A has a solution"
- this swaps the first positive implication for its contrapositive
"if B has NO solution then A has NO solution" AND "if A has NO solution then B has NO solution"
- this swaps both positive implications for their contrapositives
- this is a bold move, and I don't believe I've ever seen it used
- but it is legal

# Undecidability

Computationally impossible.

No algorithm solves the problem on every input even if unlimited time and space is given.

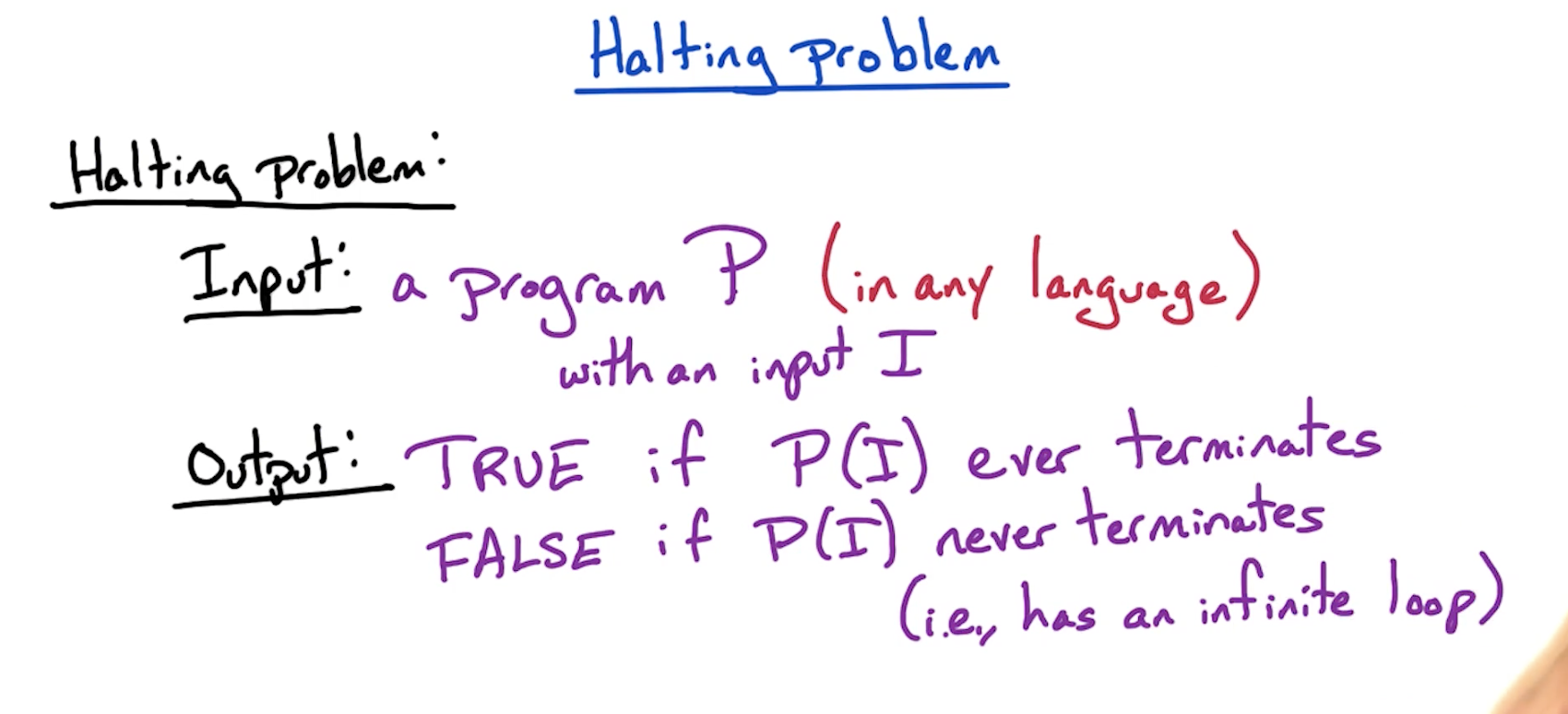
# Halting Problem

← Max Flow LP →