DP Solution Approach | Viveckh's Notepad

# DP Solution Approach

No recursion in algorithm, although you can use a recursive nature in the solution
Approach
- Step 1: Define subproblem in words (e.g. what does each index contain)
  - Operate on a prefix of the input
  - Add constraint (like including last element for LIS)
- Step 2: State recursive relation (e.g. a formula to compute the subproblem defined above, in this case, value at the index)
  - T(i) in terms of T(1), .. T(i-1). Basically inverting recursive approach
Also look up inductive hypothesis because DP is like proving hypothesis through induction.

Referring back to Robotics lectures, we should think of dynamic programming as an approach that defines a policy such that we can have an answer for every state. For example, when we are dealing with strings in the examples below, at any given state, we need to be able to compute the longest LIS or LCS for every subsets of strings, not just the originally inputtted string. And that's what the algorithms are made to be capable of. For LIS, if we were to chop the end half of the original string, we can still use the L array to know the length of LIS upto the last available element. Likewise, for the LCS problem, even if we chop the second half of string X or Y, we can still look at the multi dimensional policy array, and know the length of LCS for what's available.

# Memoization

Using hash tables to track what's computed so it doesn't get computed again.

Not going to use it in the course.

# Fibonacci Numbers

# Finding the fibonacci number

Running Time:

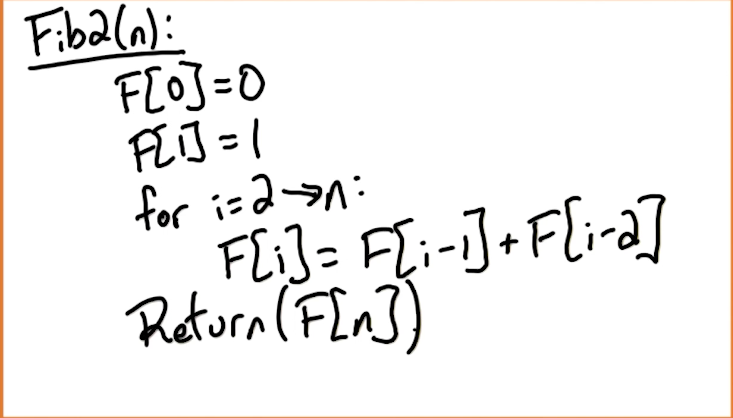
# Longest Increasing Subsequences (LIS)

substring = set of consecutive elements
subsequence = a string you can obtain by deleting elements

For example, in [5, 7, 4, -3, 9, 1, 10, 4, 5, 8, 9, 3]:

some subsequences are [5, 4, 9, 10], [4, 1], [1], [-3, 1]. But only the last one is an increasing subsequence.

We need to find the LENGTH of the longest of such increasing sequence.

Answer: [-3, 1, 4, 5, 8, 9]

# Attempt 1

Our first attempt is always going to be using the identical problem on a prefix of the input.

In this case, we're going to look at first i elements of the input array.

Let

And we're going to figure out a way to express in terms of through

So we have some interesting observations as we start to attempt this.

We are keeping a running count of the length of LIS in the L array as we proceed through the indices of A array. When we get to index i=9, the longest increasing subsequence we had been tracking [5, 7, 9, 10] suddenly becomes unoptimal since we can't append value 8 from index i=9 to it. However, an earlier suboptimal solution [-3, 1, 4] would now be optimal when it gets to index i=8-10 since the values of 5, 8, 9 would be easily appendable to this solution resulting in the final LIS to be [-3, 1, 4, 5, 8, 8, 9] with a length of 6.

So this raises some important questions our algorithm needs to answer

How do we maintain a suboptimal solution so it realizes its potential later?
Given multiple increasing sequences, which one to track?

Some things that enable this is

We need minimum ending character in LIS solution, for this, we need to maintain the length of LIS for every ending character

# Attempt 2

We are going to include the restriction that the current index i MUST BE INCLUDED while finding the length of longest subsequence so far.

This small change gives us the benefit that when we are at later stages of the array when there might be multiple LISes, we know to proceed with the sequence with the minimum ending character without knowing the sequence itself. Given the combination of A and L array, at any point as we begin populating it, we know what is the length of the longest sequence so far and what does it end in.

In this revised approach, you can see that we are tracking length of LIS differently. On , drops to 1 again because after including this index itself, the longest sequence is just . Now why do this? The approach will be obvious at step with value 8. We cross out two indexes because they have values in A array greater than 8, and since we want a LIS that includes 8, those can't be our options. Quite conveniently, that also drops one of the competing LISes that had length of 4 . Now since at index , the length of LIS is highest (4) and A ends at 5 (which is lower than 8), we take that length of LIS and add 1 to it resulting in

# Final Solution

# Longest Common Sequence (LCS)

Input: 2 strings. and

Goal: Find the length of longest string, which is a subsequence of both X & Y

Let's say we use the following two strings.

Index	0	1	2	3	4	5	6
X String	B	C	D	B	C	D	A
Y String	A	B	E	C	B	A	B

# First Attempt

# Subproblem

Designing subproblem, trying same problem on prefix of input

For i where

Let

# Recurrence

So lets say we start with the last characters of both strings. There are two possible cases:

: In this case, L(i) = 1 + L(i-1)
: In this case, LCS does not include . And if we do end up dropping one or the other from our consideration, we now have two different lengths of prefixes from X and Y.

Therefore, we need a multi-dimensional array to keep a count of the LCS such that we can define recurrence, and have length of LCS at each step of the subproblem solving. This allows us to slide the window of prefixes essentially of both strings and for each state have a count.

# Second Attempt

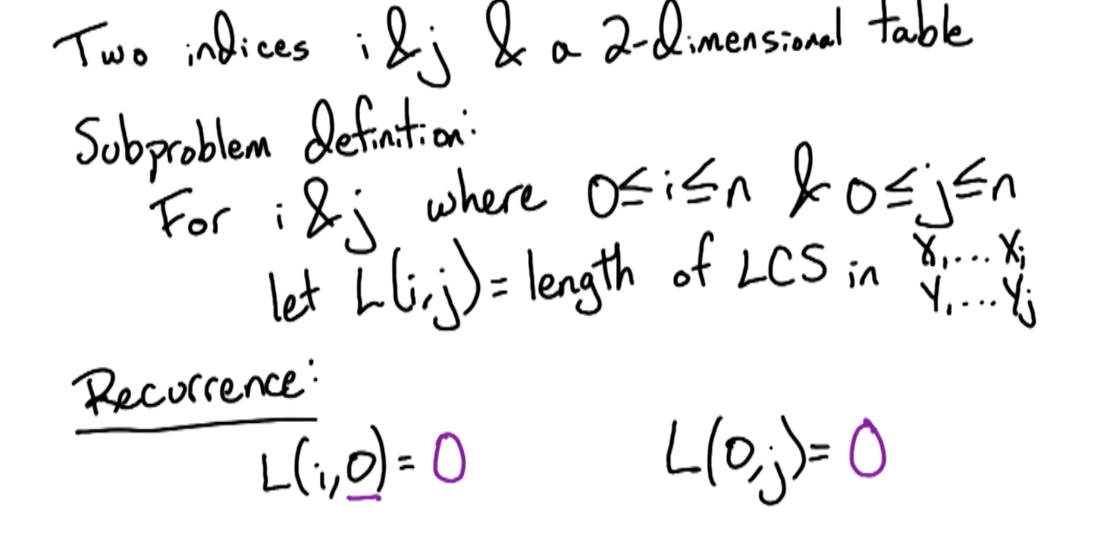
So now addressing the two possible cases we were trying to address in the first attempt, but using this new multi dimensional array we have to track LCS length.

i and j are used to denote corresponding indices in the X and Y arrays.

: In this case, L(i, j) = 1 + L(i-1, j-1). This works because if the current element in consideration in both X and Y arrays match, it is fair to add 1 to the previous LCS length.
: In this case, LCS does not include .
- If we drop , then . Because the current x element is being dropped, so LCS for previous x element is good to carry forward.
- If we drop , then . Because the current y element is being dropped, so LCS for previous y element is good to carry forward.
- But which one do we pick, we take the max of the two expressions above. Therefore,

# Final Solution

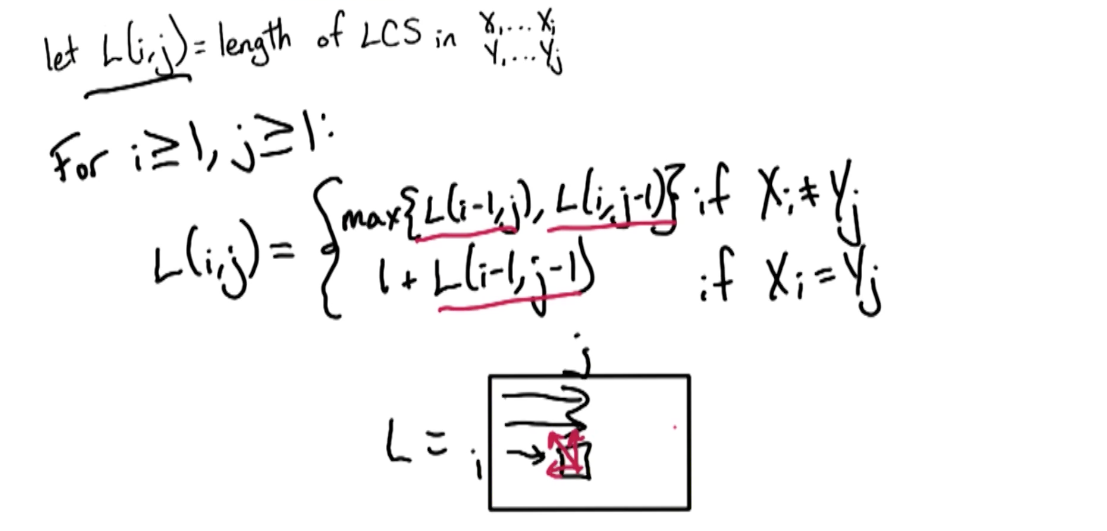
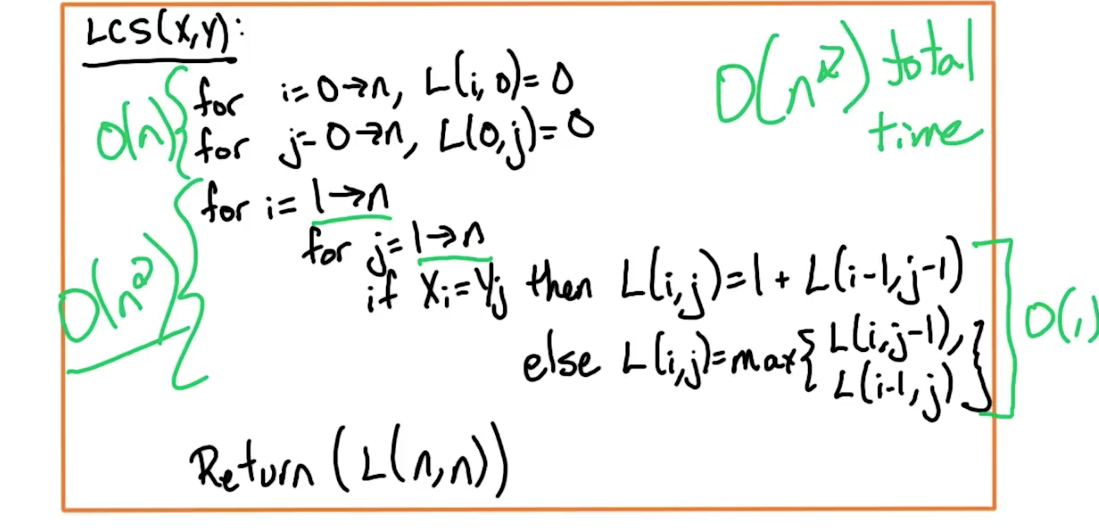
# Practice Problems

# LCS Length Table to LCS

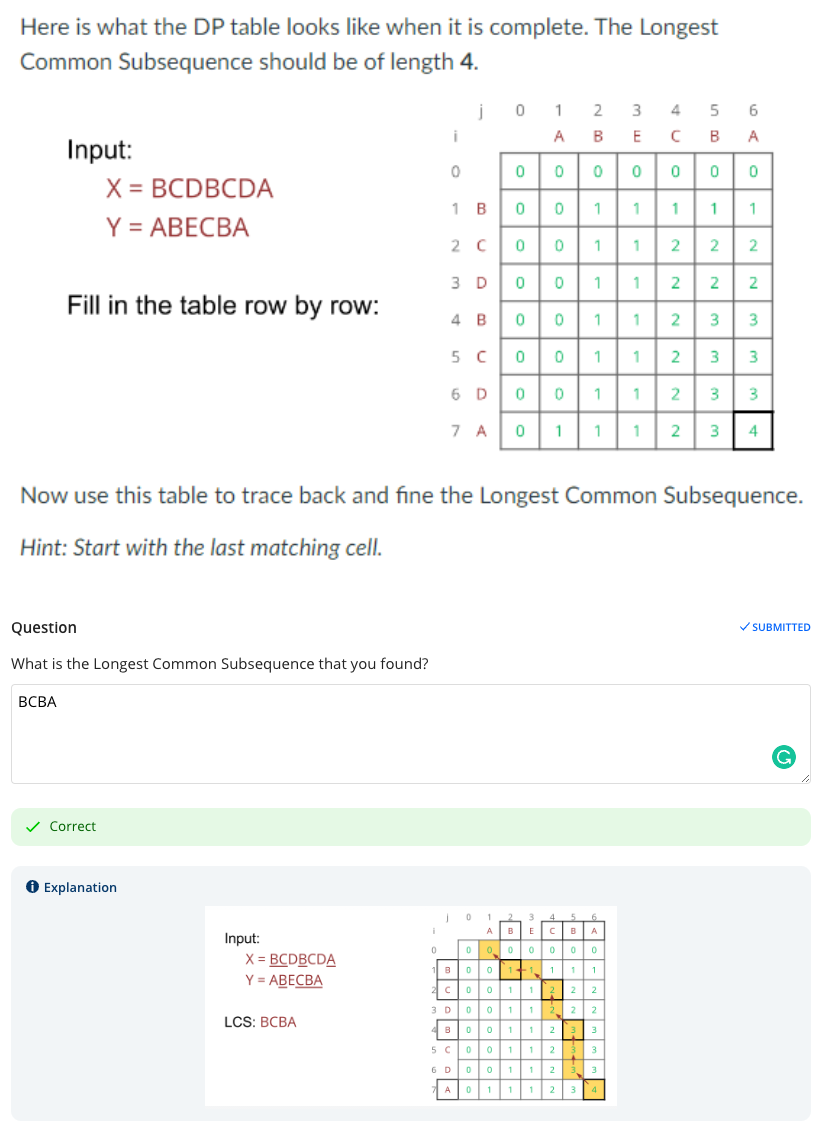
In this above question, since the original multi dimensional array is populated row by row, we are traversing from the bottom right corner back to the top left to find the LCS. We are essentially looking for the first occurence of each number and each of such cells is the intersection point of another matching letter. In this case, the first occurence of 4 gives of A, first occurence of 3 gives us B, first occurence of 2 gives us C and first occurence of 1 gives us B. We reverse that and get BCBA.

Another approach that worked for me is just looking at the last column. And finding each cell where a new number shows up for the first time. But not sure how reliable it is.

# Contiguous Subsequence/substring (6.1)

# Hotel Stops (6.2)

# Yuck Donalds (6.3)

# String to words (6.4)

# Longest Common Substring (6.11)

# Knapsack Problem

Input:

n objects with integer weights and integer values .
Total capacity of the sack is B

Goal: finding subset S of objects that maximizes the value V while staying within the total capacity of B

Two versions

One copy of each object - without repetition
Unlimited supply of each object - with repetition

# Greedy Appproach

Sorts the object by
And then iterate in this sorted order picking up the objects until capacity is filled
Fails to find optimal solution.

# Attempt 1 (No Repeat)

Step 1: Define subproblem k(i) = max value achievable using a subset of objects 1, .., i
Step 2: Express k(i) in terms of

Sample set

B=22

Index	1	2	3	4
Values	15	10	8	1
Weights	15	12	10	5
k	15	15

But this prevents us from seeing the combo of 10+8=18 from index 2 & 3.

Take suboptimal solution to i=2, taking 10 value from there would've allowed us to take on the 8 from index 3 adding up to 18 total value.

(to fill in k2) would've allowed us to see potential of index 2 and 3.

# Attempt 2 (No Repeat)

To solve , we couldn't use

Needed with the additional restriction

So we will use two parameters i & b

If we include the object $i$ , we get value v_i and add that to the best solution so far i.e. . i-1 and b-w_i because we are taking previous subproblem's best solution. Basically, saying what was our best solution from the multi-dimensional array assuming we include the current new object. If this new object takes up weight w_i, what is the best solution looking back at position i-1 of k with weight capacity left for b-w_i.

if we do not include object $i$ , we just carry on with the previous subproblem's best solution i.e. . The i-1 because we are carrying on with previous subproblem's solution. The b is left as is because since we are not including current object, the weight capacity available remains as is.

# Pseudocode (No Repeat)

# Poly Time?

The running time is not polynomial in the input size. Because to represent B takes space O(logB). That is why it is NP complete.

Concise explanation by Kun Yu

I was stuck on the same question for a while, here is how I convince myself now:

When B is 8, the input size is n items + 3 bits, running time is 8n.
When B is 16, the input size is n items + 4 btis, running time is 16n.
When B is 32, the input size is n items + 5 bits, running time is 32n.

This shows that when input size increases just 2 bits, the running time increases 4 times from 8n to 32n, this is how the running time is exponential in the input size.

# Knapsack (Repetition)

For the second part of the max, the condition that needs to be fulfilled is

# Knapsack (Simpler subproblem Repetition)

# Practice Problems

# 6.17, 6.18, 6.19 (Change making)

# 6.20 (Optimal BST)

# 6.7 (Palindrome subsequence/substring)

# Chain Matrix Multiply

Todo: Need to understand this better by coming back

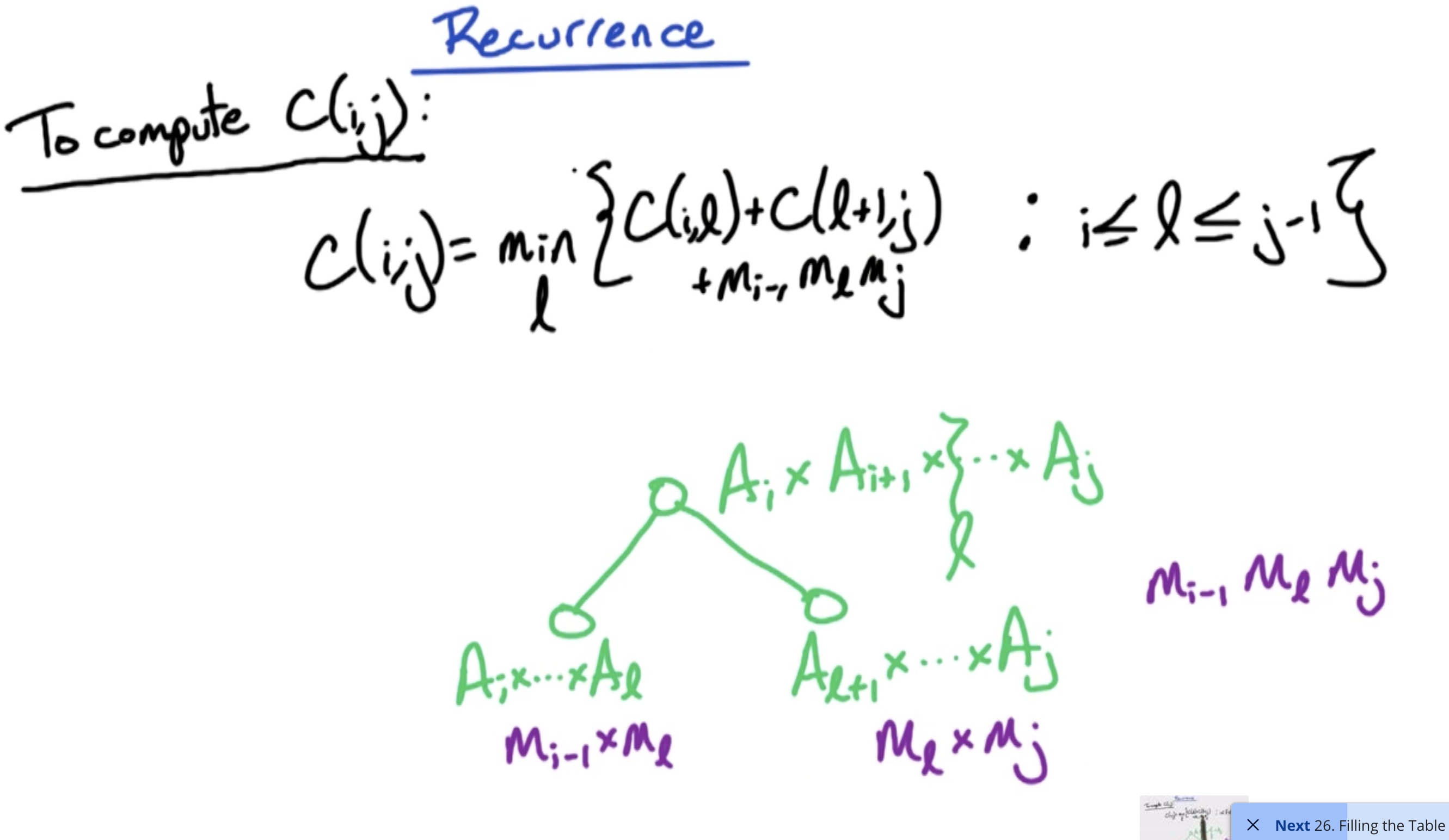
We are only filling up one side of the matrix diagonal - the upper side of the diagonal. That's why we have the nested for loops operating differently.

← Introduction Shortest Paths →