# Useful Reads
Great visulization to understand Ford-Fulkerson
The lectures made much more sense after watching the above video
# Algorithms
- Ford-Fulkerson
- Edmonds-Karp
# Max Flow Problem
# Input
The input to the Max-Flow problem is a Flow Network. A flow network is a directed graph G = (V, E) where vertex s is the source vertex and t is the sink vertex.
For each
# Computation
We need to compute flows for each edge in the flow network such that supply can be sent from vertex s to t while maximizing the amount sent without exceeding edge capacities.
The following constraints must be met:
- Capacity constraint: for all
- Conservation of flow: for all
, flow-in to v = flow-out of v
# Goal
Find a valid flow of maximum size:
size(f) = total flow sent = flow-out of s = flow-in to t
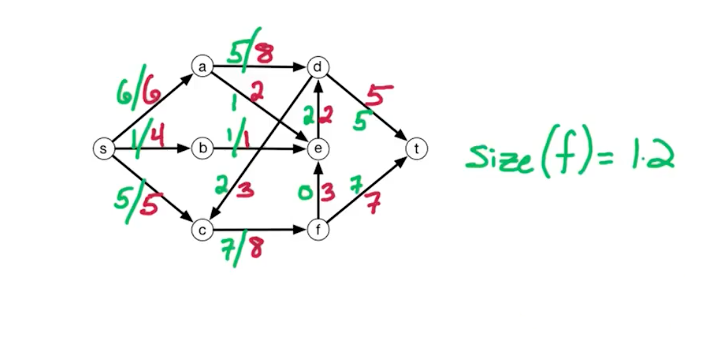
In the example above, the edges represent
The size(f) is 12 since the two incoming t add up to 12.
# Concepts
- Having cycles is okay in a flow network. We might/might not use part of it depending on if it allows maximizing
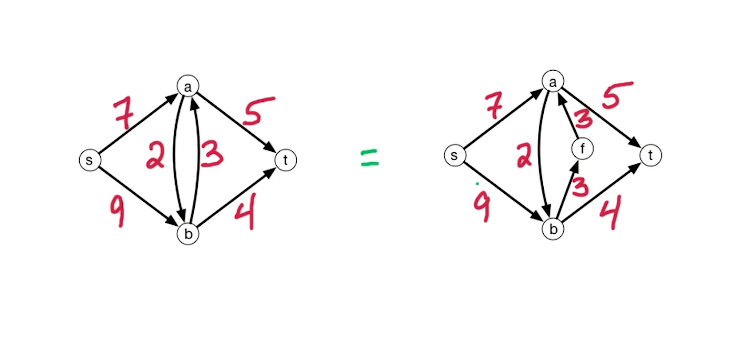
- Anti-parallel edges like shown below on the left are not okay for a flow network, as it makes it difficult while constructing a residual network later as it needs to add identical edges on the opposite direction. So we need to rewrite such edges like shown below on the right
# Residual Network
Given the input of the flow network G = (V, E) with edges and weights as described in input above, and flow
if
and then, add to with capacity if
and then, add to with capacity (Backward Edge)
This entire concept is explained better in this video
# Ford-Fulkerson Algorithm

# Running Time
Assume all capacities are integers, then flow increases by >= 1 unit per round.
Let C = size of max flow, then <= C rounds exist.
Since each round requires O(m) time, the total runtime is O(mC)

However, this assumes that the capacities are integer values and the running time depends on the size of the max flow. Therefore, it is said that the run-time is pseudo-polynomial, similar to that of Knapsack where the size decides the runtime. To address this, we have other algorithm like Edmonds-Karp.
# Verifying max-flow
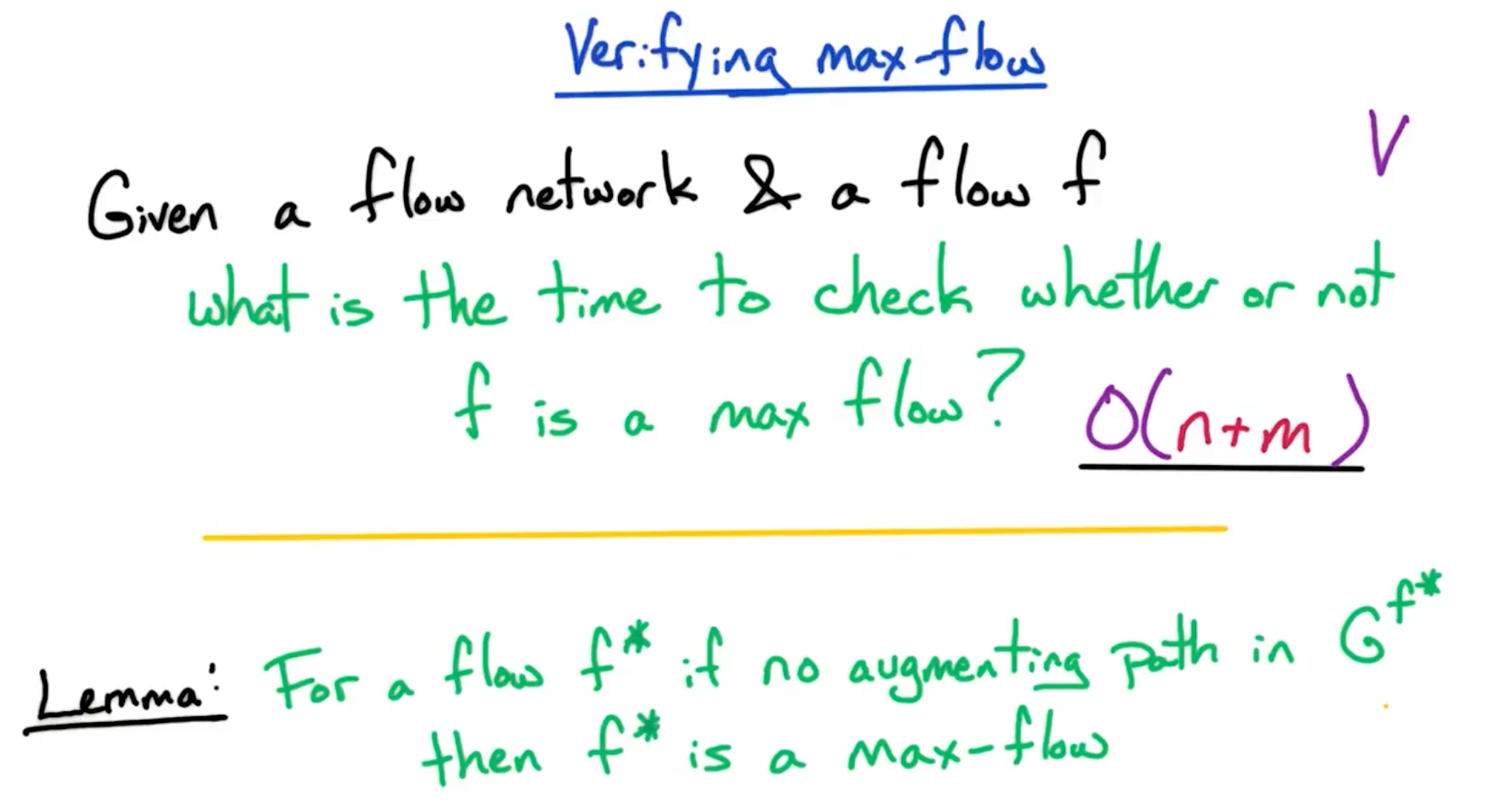
- Build a residual graph O(n+m)
- Check path from
in residual graph - Run DFS from s to see if a path exists to t.
- If no path exists in the residual graph from s -> t, then this is the max flow.
# Min-cut Problem
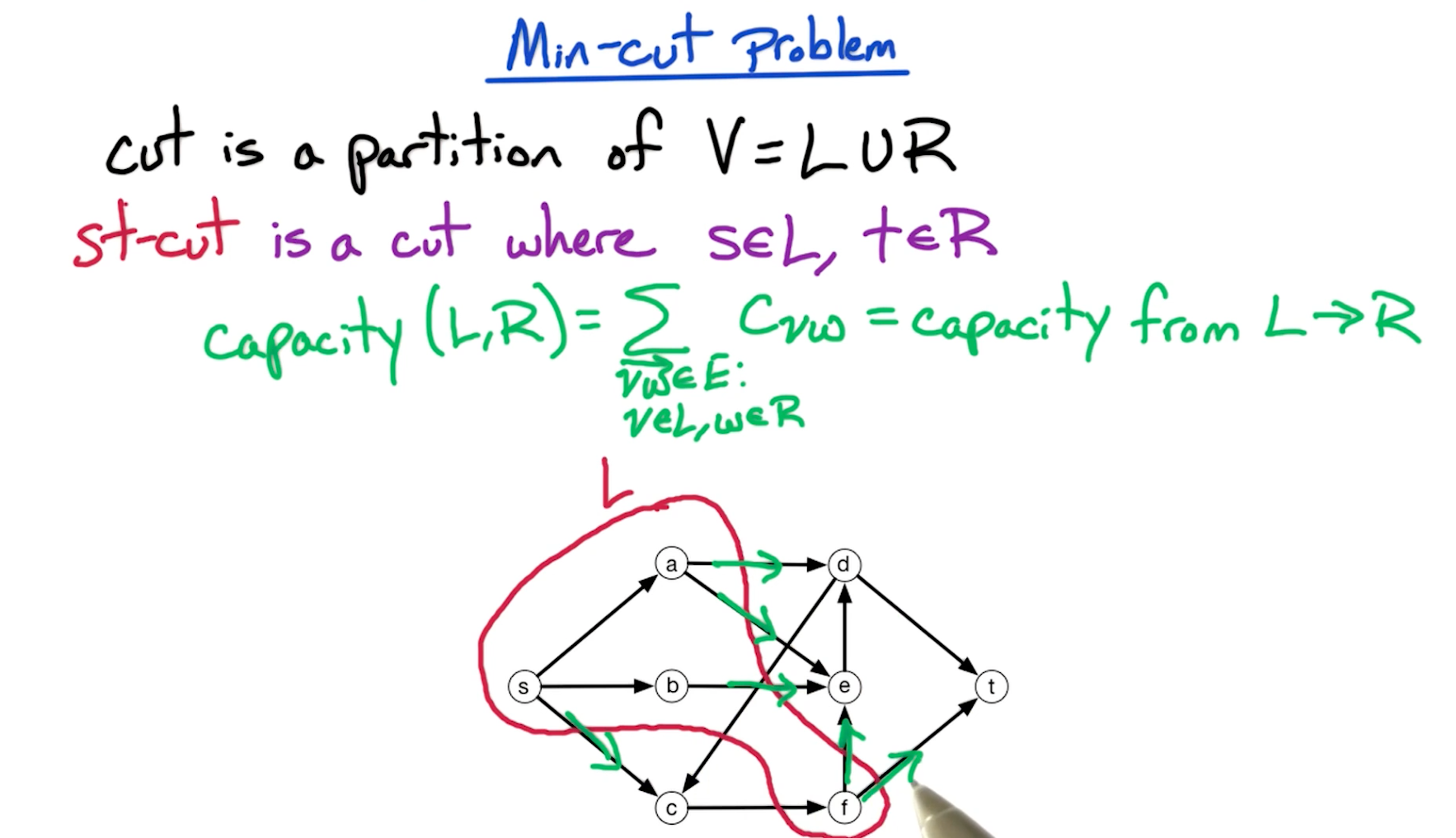
Note that the vertices do not have to be connected for them to belong to either L or R. For e.g. vertex
fis not connected toaorbin the L cut above.We only care about the outgoing edges from the cut highlighted in green.
# Input/Output
Input: Flow Network
Output: st-cut (L, R) with min capacity.
By a st-cut with min capacity, we mean a cut such that it yields the minimum sum of capacities of all outgoing edges from L cut towards R cut. The example cut shown above doesn't get the minimum capacity though, it's just one of the example cuts.
# Max-flow Min-cut Theorem
Explained well in this video after 17:30
Thereom:
To prove this theorem, we are going to prove two relations.
If both the above relations are proven, then that infers

To prove the first equality below,
We get the 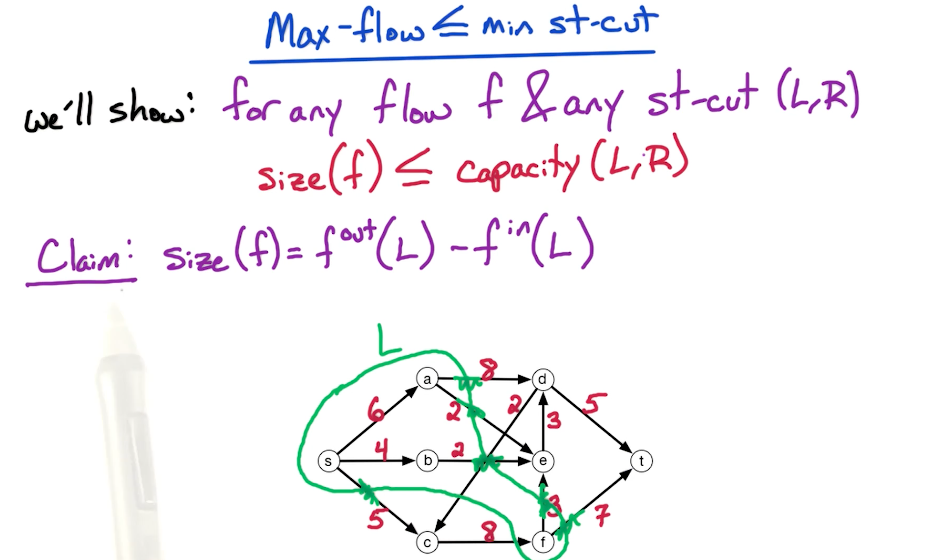
To prove the second equality below,

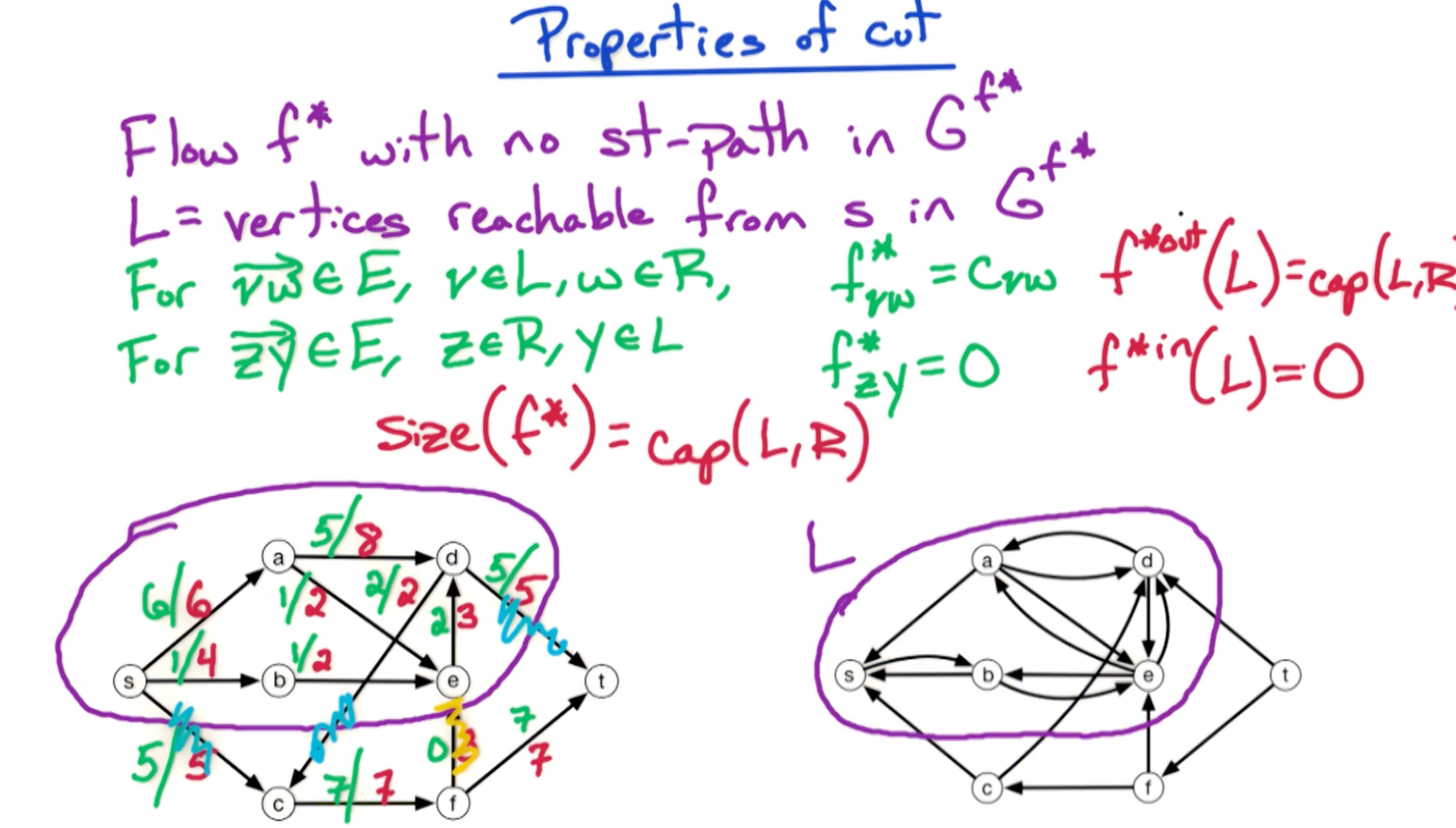
# Properties of Cut
After the flow is filled (left graph), we can create a residual graph of forward and backward edges (right graph). We can construct this using the logic below.
- backward edge present: if positive flow exists in an edge
- forward edge present: if capacity is leftover in an edge
In short, fully capacitated edges are only one-way.
Then, L is the set of vertices reachable from s in the residual graph.
And R contains the remaining edges.
Tip: All the edges leaving L have to be unidrectional (and hence fully capacitated), otherwise, they'd have a way back to L and if that's the case, they'd have to be included in L.
# Image Segmentation
# Parameters

# Example
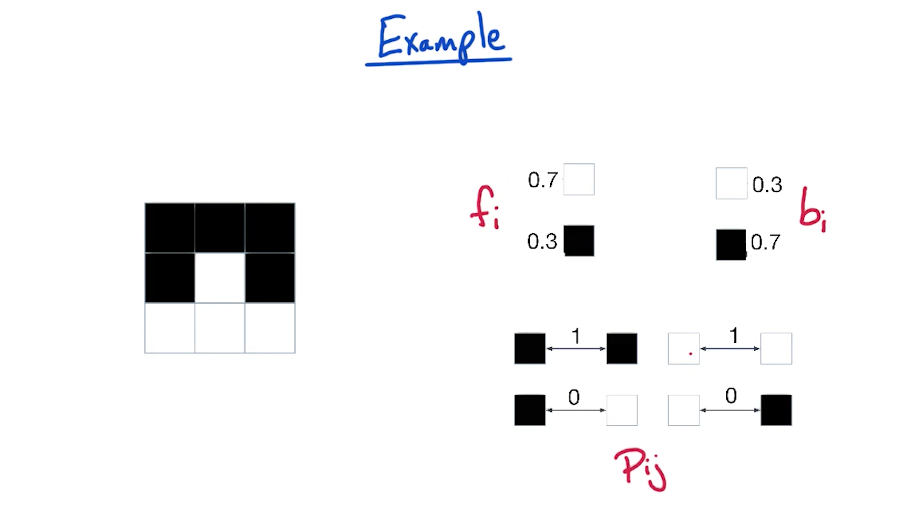
# Partition

We have to reformulate this to a min-cut problem, for which we need to get rid of the negative sign in the expression.
# Reformulation
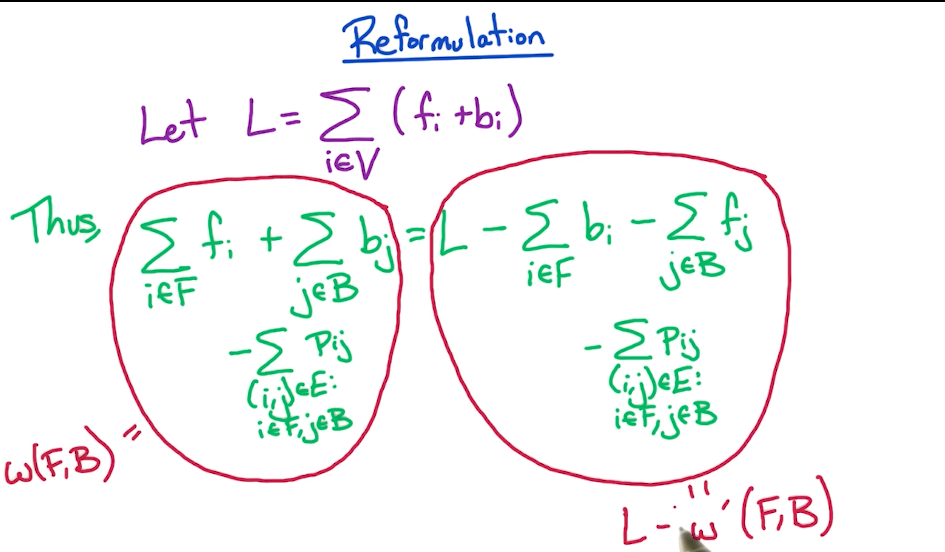
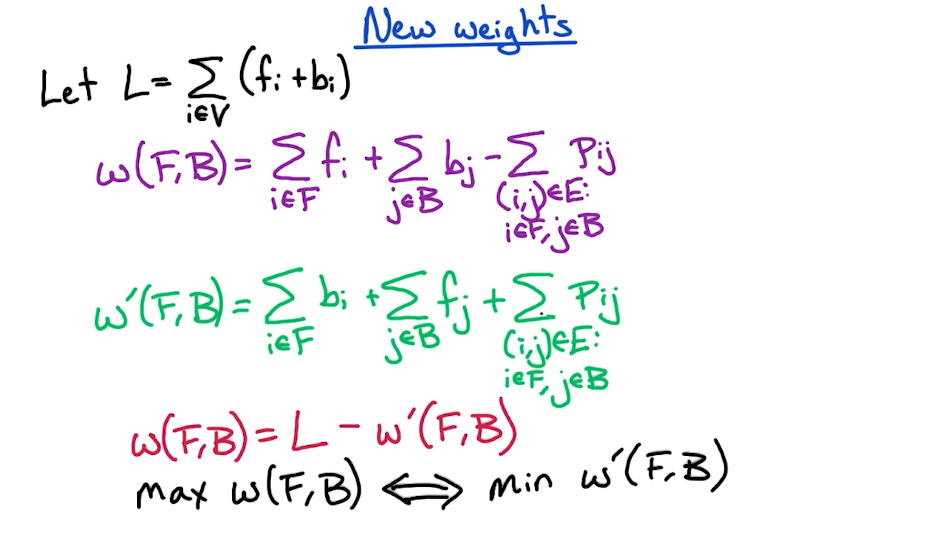
# New Problem

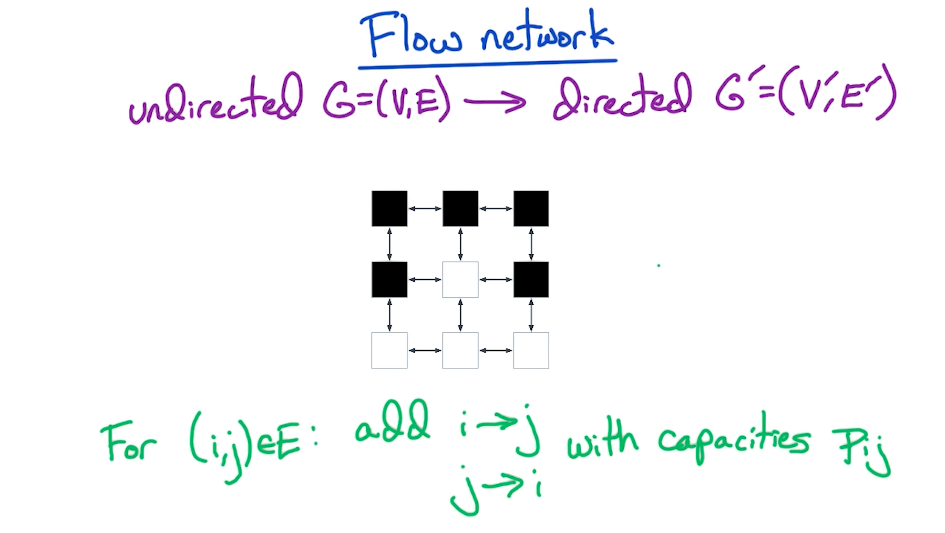
# Foreground and Background
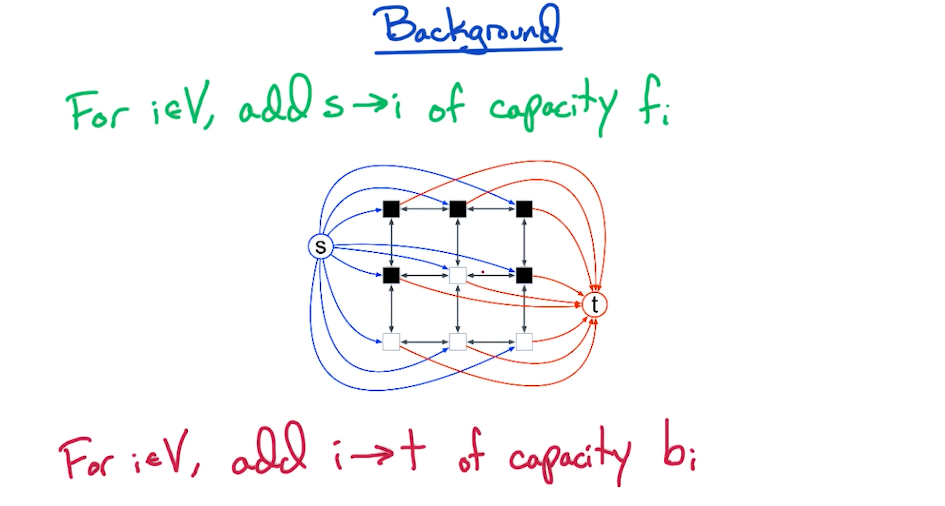
# Cuts
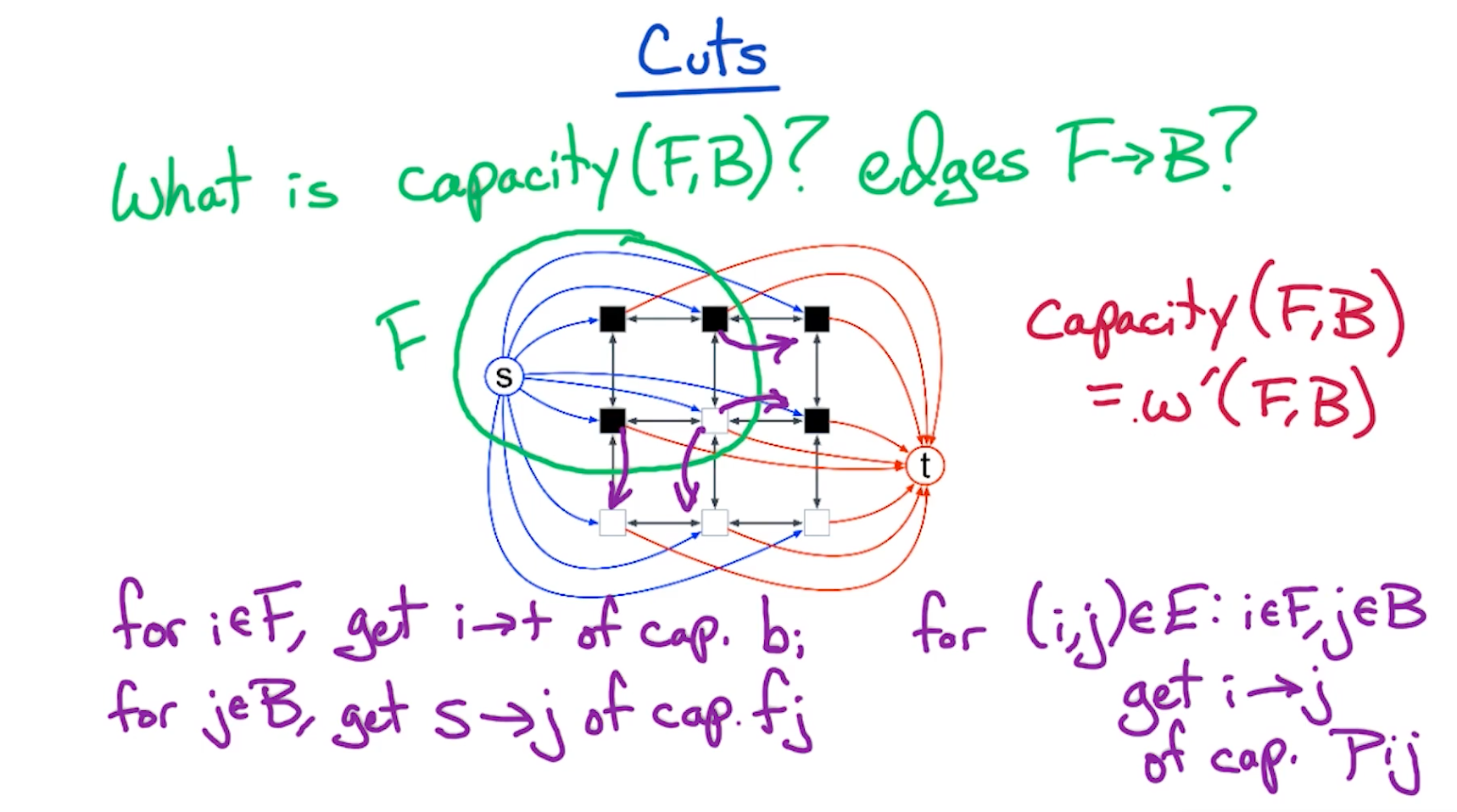
# Solution
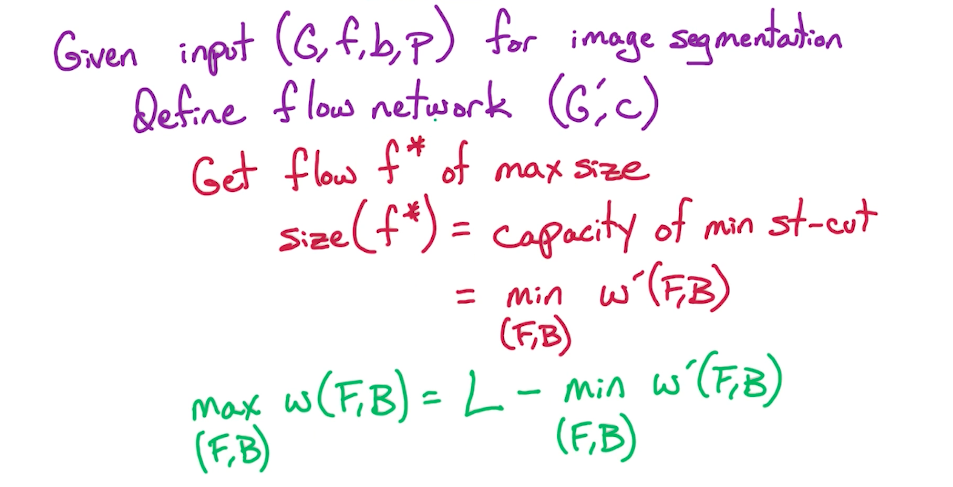
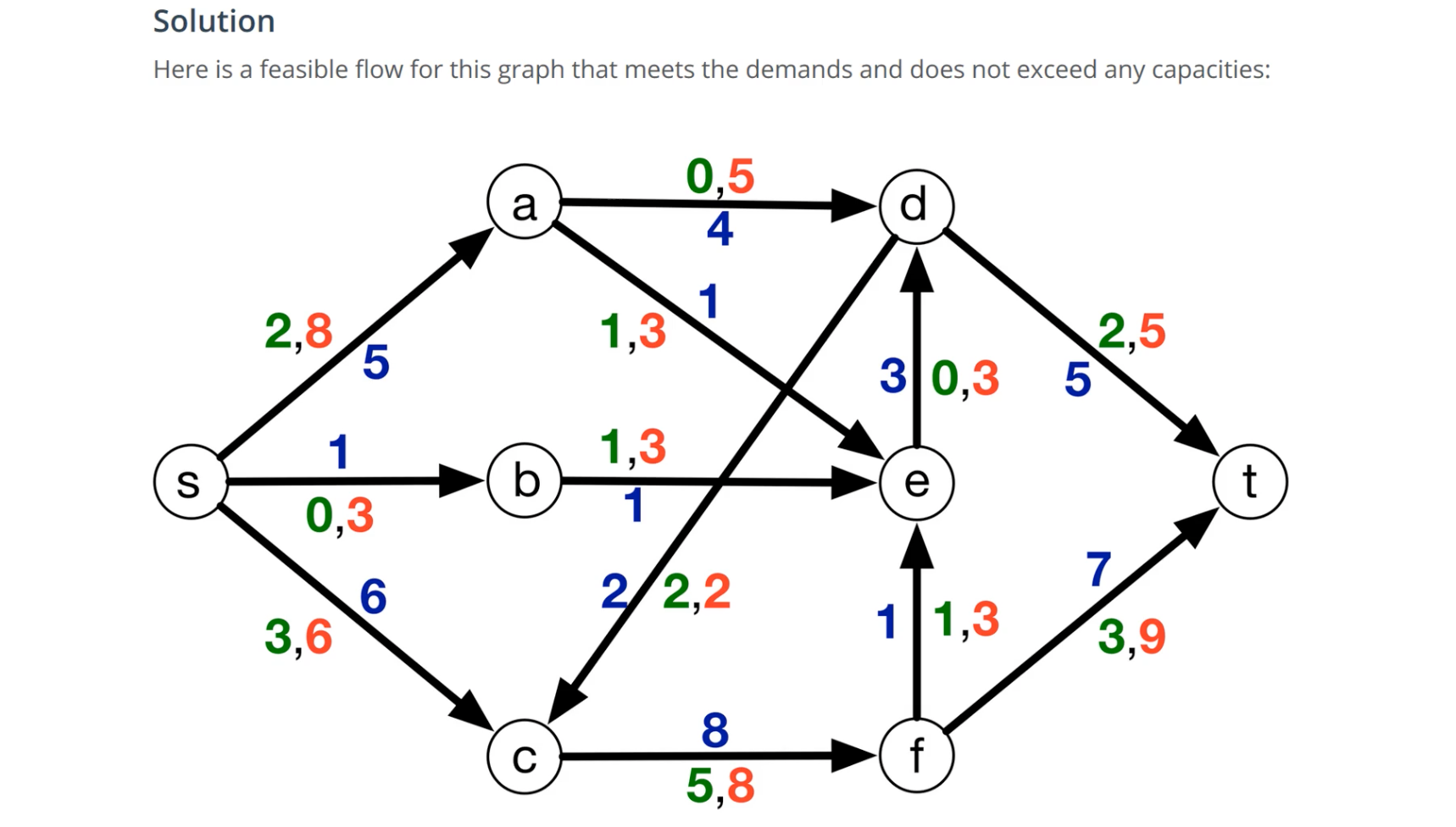
# Generalization / with Demands

In the below example, the blue values are the flow values which is derived from the demand and capacity given in the format (demand, capacity) in each edge.
Tip: The idea is, in each edge, the flow has to meet at least the demand, and at most the capacity.
# Reduction
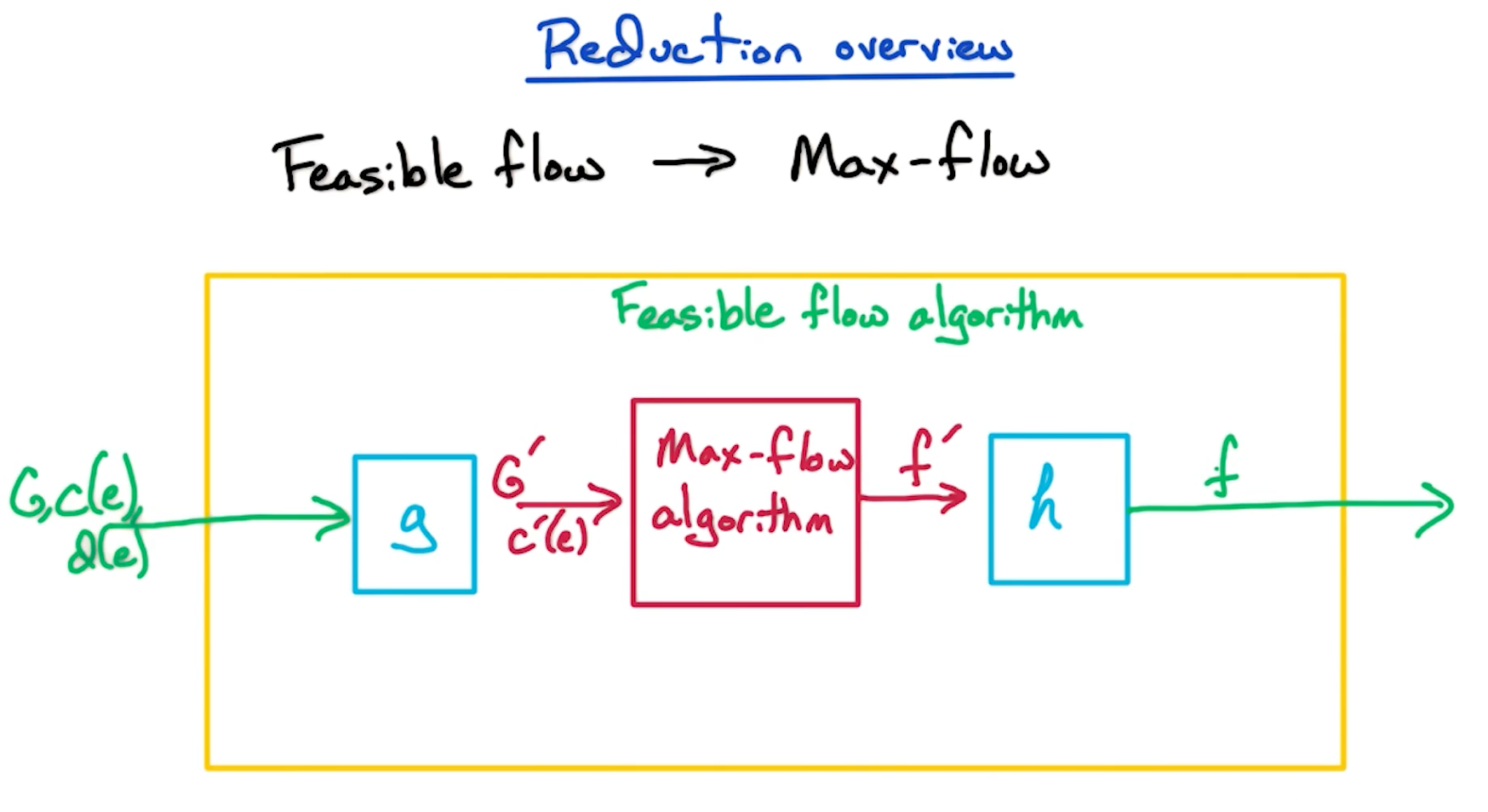
The general idea is taking the input to the feasible flow problem (graph , capacities g. Then we run the max-flow black-box algorithm with these transformed inputs and generate the output. The output then again needs to be transformed to a feasible flow output using the h function.
Haven't been able to figure out the h part.
Following is the general algorithm for a g function that is supposed to construct
- Take the original set of vertices
- For each
, add to with - Add two additional vertices
and - For
, add edge with - For
, add edge with - Add edge
with
Upon following these steps, we form a 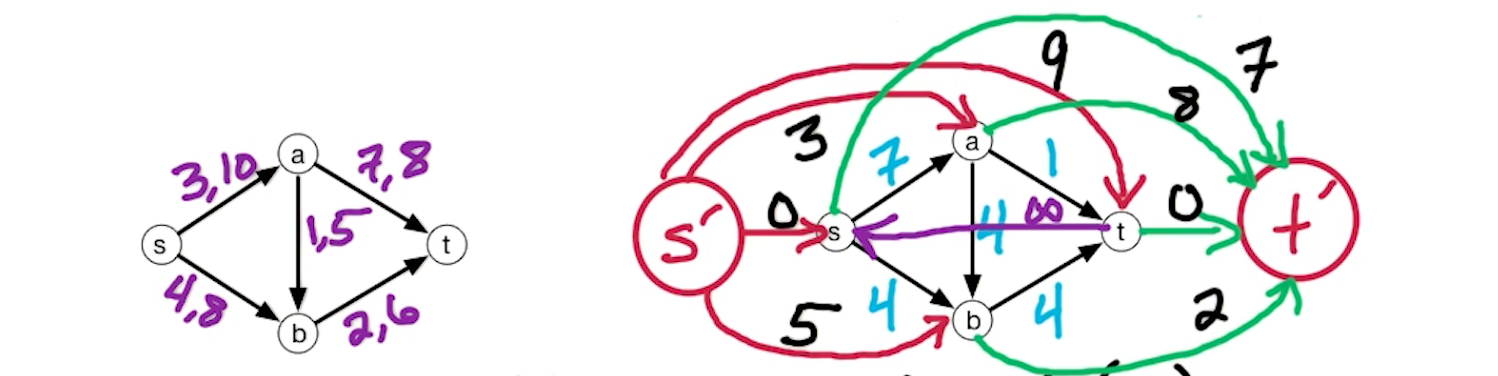
Now we run max flow on the generated h. When flow
# Some additional tips:
Intuition for original edges 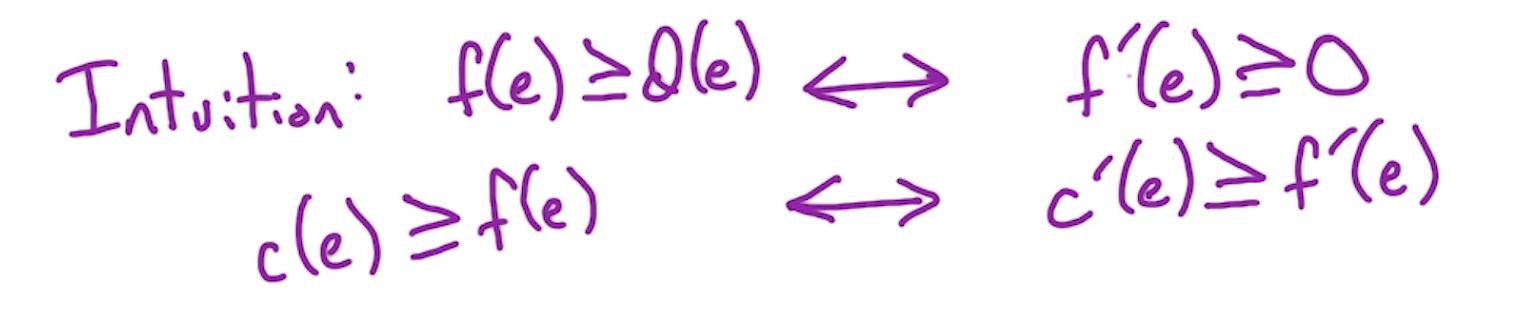
# Saturating Flows
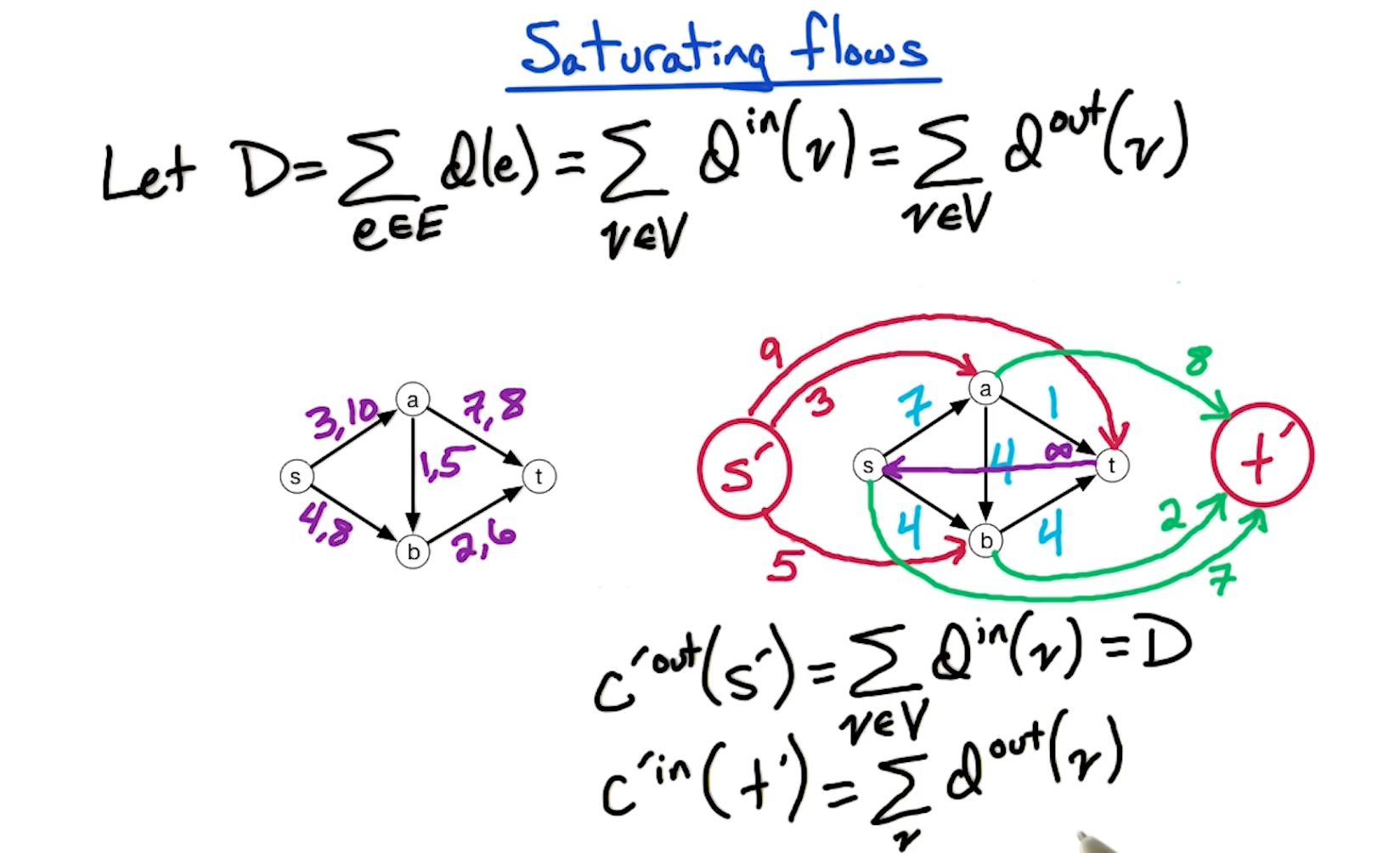
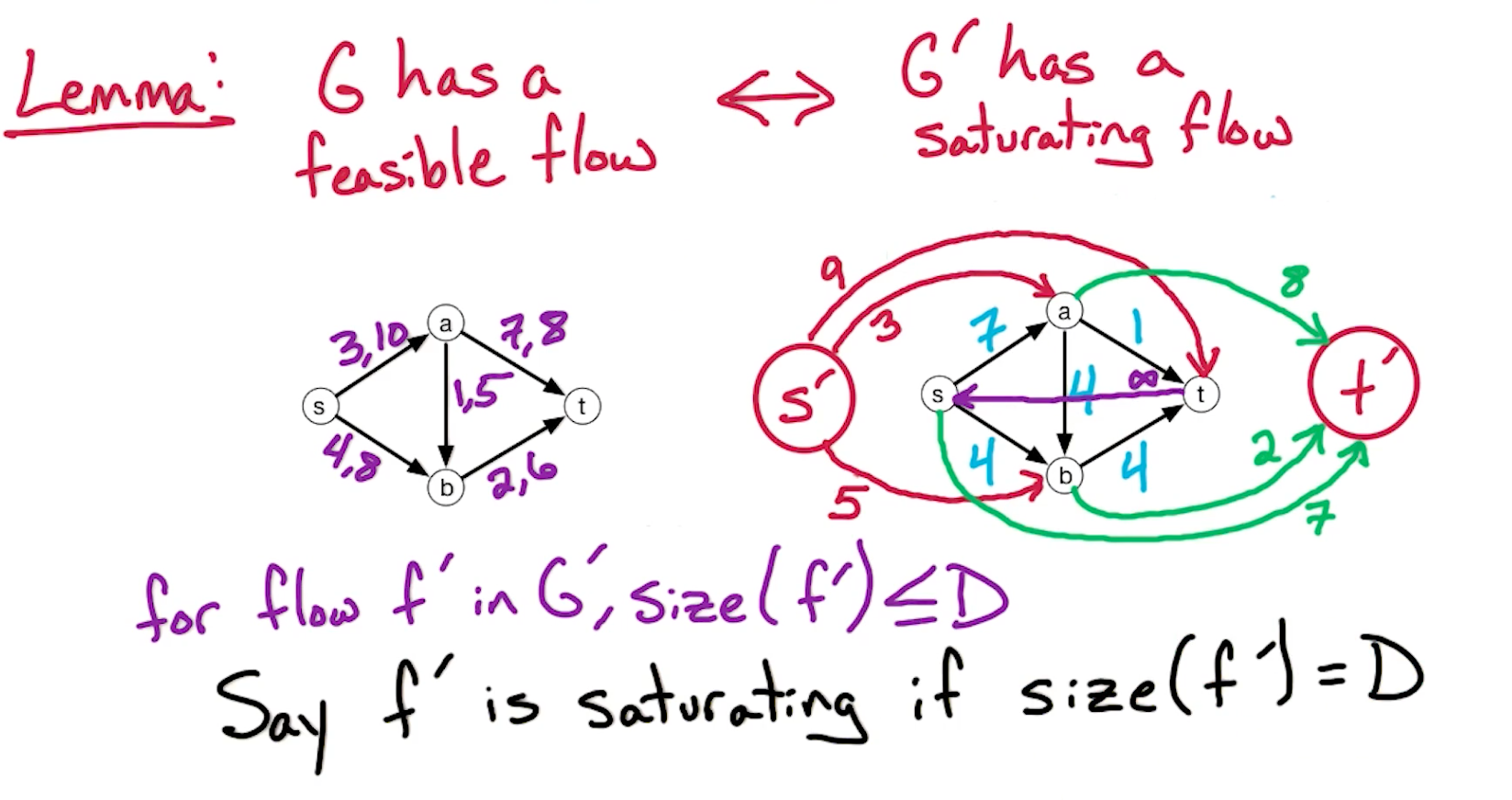
How to show a saturating flow is feasible?

- To show
f is valid, we need to show- flow-in = flow-out for all vertices in G created above,
- flow along an edge is not higher than the capacity
- To show
f is feasible, we need to show- all the demand consraints are satisfied
How to show a feasible flow is saturating?

Not sure of the following
- To show
is valid, we need to show - flow-in = flow-out for all vertices in G created above,
- flow along an edge is not higher than the capacity
- To show
is saturating, we need to show ...
# Max Feasible Flow

# Edmonds Karp Algorithm
- Identical to Ford-Fulkerson except a few differences
- Ford-Fulkerson finds augmenting paths using DFS or BFS, Edmonds-Karps uses BFS.
- Ford-fulkerson's time complexity is
where C is size of max flow. The time complexity of Edmonds-Karp is - Ford-fulkerson assumes integer capacities whereas Edmonds make no such assumptions
# BFS Properties
Lemma: In every round, residual graph changes (>=1 edge deleted). For every edge e, e is deleted and reinserted later
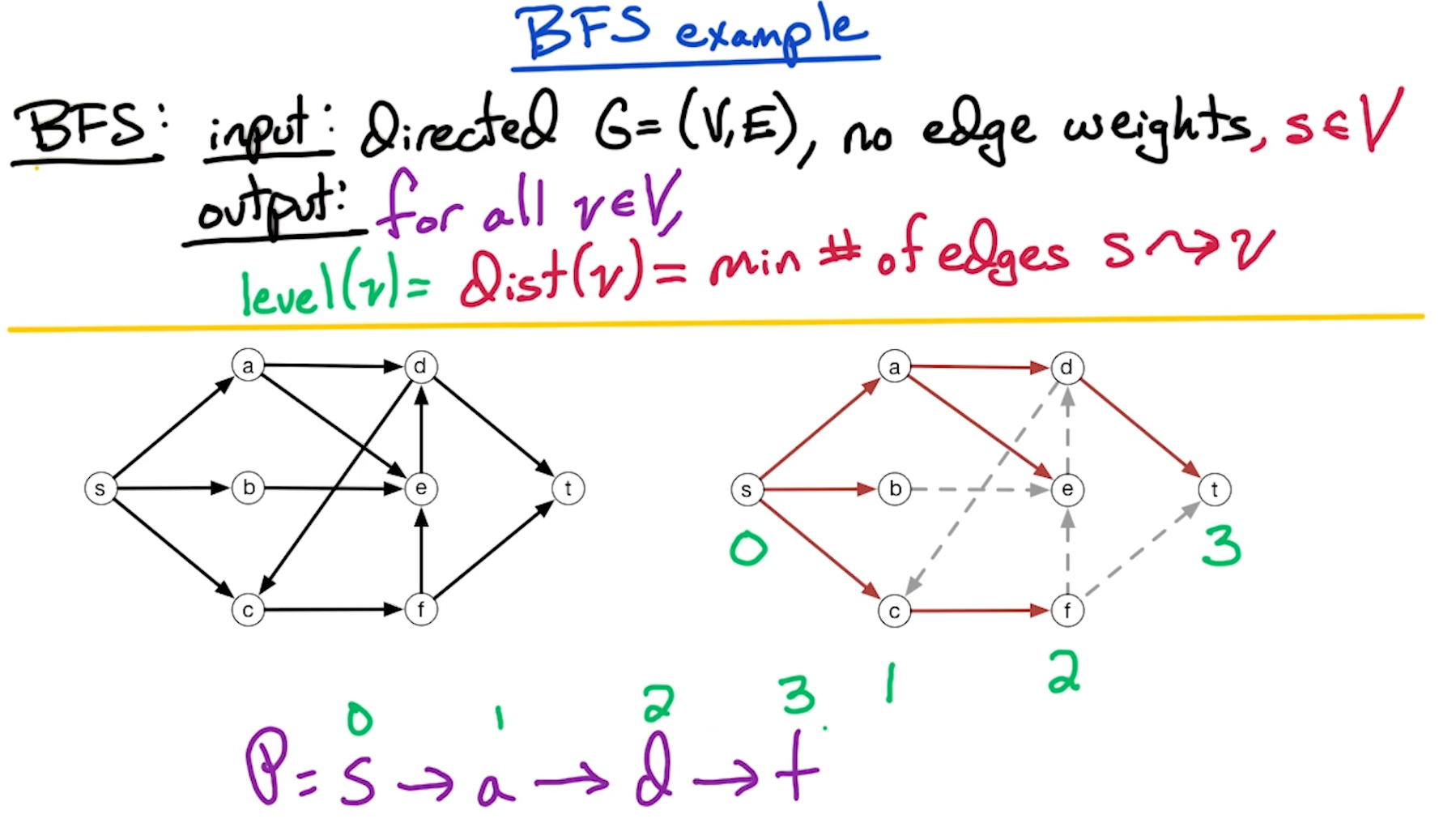
In the above example, the numbers correspond to the level of the graph. Since BFS expands equally in all directions and explores all unvisited nodes at a level before moving to the next level, this illustration is helpful to understand.
Claim: For every
Claim: If we delete
# Residual graph change

To get an intuitive sense for this, first understand what a "residual" graph means. A residual graph is tracking the residue or left over capacity. So:
- If a forward edge exists along an edge, it means there is capacity left along that edge.
- If ONLY forward edge exists, that means all of the capacity is remaining along that edge.
- If a backward edge exists, it means some of the capacity is used by flow.
- If ONLY backward edge exists, that means all of the capacity is used by the flow, and no leftover capacity exists.
Now based on this understanding, re-evaluate the above picture and it might explain when a forward or backward edge should be added or removed.
← Satisfiability NP →
