Viveckh's Notepad

# Basic Strategy

  • Create a data structure (a graph) that facilitiates path planning (discretize if necessary)
  • Quantize the agent and goal locations to the graph
  • Perform path creation with a search algo
  • Localize the path back to game world
  • Optionally clean up the path to look more natural
  • Move the agent to follow path until goal is reached

# Path planning algos

Computational issues: Completeness, time and space complexity, optimality

# Search strategies

  • No domain knowledge, only goal state is known
  • Example: DFS, BFS
  • Domain knowledge represented by heuristic rules
  • Heuristics drive low-level decisions

# Grid Lattice

# Generation

  • Verify world boundaries don't go through grid lines
  • Verify no obstacle point within a grid cell, or vice versa
  • Verify obstacle edge does not intersect grid cell edge
  • Sometimes useful to mark both edges and cells as traversable (can help agent get back on navigable grid if on a partially blocked cell. For e.g. where obstacles block one wall of the grid cell but the cell itself is still navigatable and other walls are still open)

# Search efficiency

grid-lattice-search-eff

  • Can return a good result if edges are all same weight or unweighted

# BFS Performance

  • Completeness: will always find a solution if there is one
  • Optimality: optimal, but only if all edges equal weight. otherwise, no.
  • Time: where b is the branching factor and d is the shallowest depth for goal node
  • Space:

# DFS Performance

  • Complentess: will always find a solution if one exists (finite map), unless max search depth is imposed smaller than map
  • Optimality: not optimal
  • Time: O(m) where m is max node depth for DNS finite map and b is branching factor
  • Space: O(bm) - closed nodes can be freed if all descendants are fully explored (Variant version is )

We can add bias for certain directions if we choose to. for example

  • by selecting vertical movement more than horizontal
  • can make paths tighter by selecting nodes found in open set more often than unassigned nodes

# Dijkstra's Algorithm

  • Keep track of costSoFar (g) as metadata at each node
  • Expand nodes with lowest costSoFar (g) each iteration
  • Graph weights would have to be positive
  • If an open set node is revisited from a different fromNode then check if the original route or new route is shorter (revise if shorter)
  • Think of Dijkstra as an adaptation to BFS, where BFS expands the nodes assuming equal weights, but Dijkstra's algorithm takes into account the cost of getting to a node to decide if it is wise to expand further
  • Uniform Cost Search is a variant that stops at goal

# Performance

  • Complentess: will always find a solution if one exists
  • Optimality: yes

# A Star

  • Combine concepts from Dijsktra and Greedy Algo together
  • Select nodes on a combined heuristic of cost so far (g) and heuristic estimate to goal (h)
  • g(n) + h(n)
  • Also talked about in AI for Robotics
  • Priority Queue/Heap is ideal for implementing since removing smallest element and adding new element take O(log n). Bucketed Priority Queue can also be considered but requires fine-tuning, often not worth the trouble
  • If a goal node cannot be reached, A* algorithm can be modified to return closest node by searching the closed set for the node with the lowest heuristic score.

# Heuristic Function

  • If you underestimate completely using heuristic h(n)=0, we get Dijkstra's algorithm
  • If yet set g(n)=0, then with a decent heuristic, we get Greedy Best First
  • Computational performance is important for heuristic, e.g. manhattan distance would be computationally efficient than euclidean since it is simple subtractions and does not involve square roots

# Admissible Heuristic

  • One that NEVER overestimates the cost to reach the goal
  • Euclidean distance is the standard admissible heuristic for path finding
  • Manhattan distane can be admissible for 4-way grid movement
  • Inadmissible does not mean "wrong", sometimes even overestimating can make A* faster if they are almost perfect

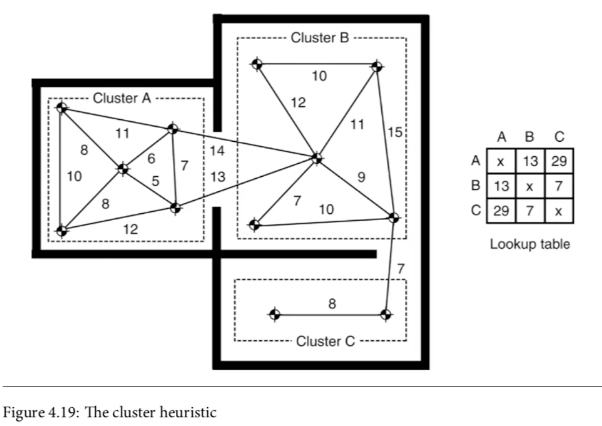
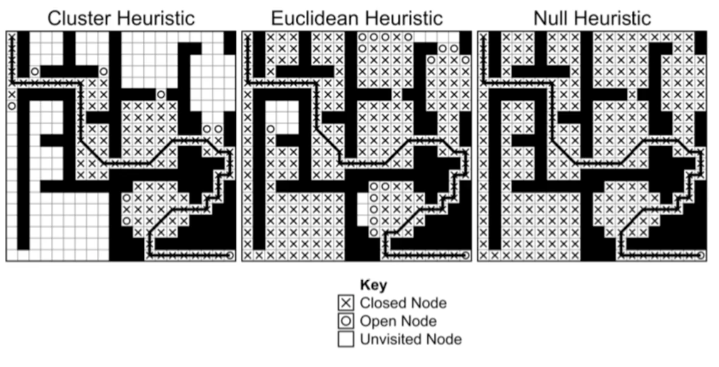
# Cluster Heuristic

  • In some cases, cluster heuristic might perform much better than Euclidean in a setting that has a lot of "rooms"

The cluster between one cluster to another is precomputed using a single representative point in each clusters. This can lead to overestimating the distance in cases since the distance between actual points might be smaller. cluster-heuristic

cluster-heuristic-comparison

# Performance

  • Completeness: will always find a solution in finite space
  • Optimality: optimal, if heuristic is admissible
  • Time: where b is the effective branching factor influenced by heuristic and d is the shallowest depth for goal node
  • Space: roughly same as Dijkstra

# In Gaming

  • Popular is games but uses a lot of memory and doesn't work well in dynamic environments
  • Maybe worthwhile to investigate variants such as iterative deepening A*

# Millington A*

millington-a-star

# Quadtrees

Given the problem of inefficient space representation in Grid Lattice, can it be improved upon?

The aim is to maintain simple convex structure but reduce storage costs. To achieve this, we can use low resolution discretization for large uniform regions. Use high resolution discretization around environment details that affect agent movement.

# Building Algorithm

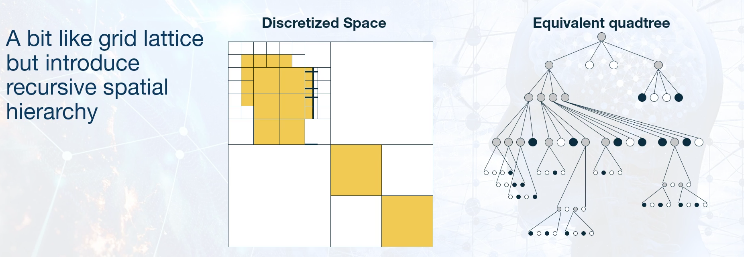
quadtree

Start with a big square region and you subdivide a cell as long as there is a mixture of traversable/untraversable within a cell.

  • Are there any obstacles within the cell?
    • If yes
      • Is the cell entirely contained with the obstacle?
        • If yes, (Untraversable condition met) stop subdividing this cell further
        • If no, (Recursion condition met) then you subdivide the cell to four children and ask the top question again for each of those cells
    • If no, (Traversable condition met) stop subdividing the cell.

# Challenges

  • Complicated data structure and parsing
  • Difficult to determine non-sibling neighbor cells
    • Requires negotiating tree structure
  • Path quality generally requires postprocessing
  • Poor discretization: Can result in undesirable quad tree subdivisions if obstacle details don't line up with quad tree cell boundaries
    • Can be bad with buildings
    • Games can enforce quad boundary level design

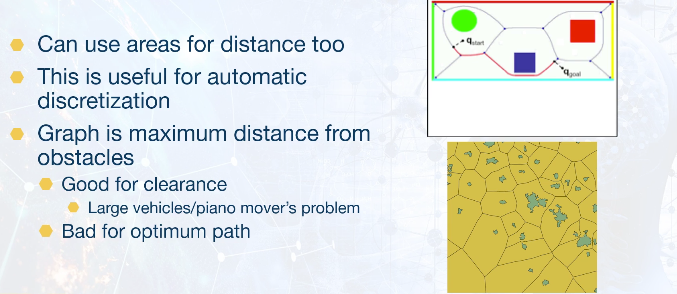
# Voronoi-Dirichlet Diagrams

  • Regions that are closest to points in a set
  • Boundary edges are equidistant from two points
  • Diagrams often shown with a single generator point per region

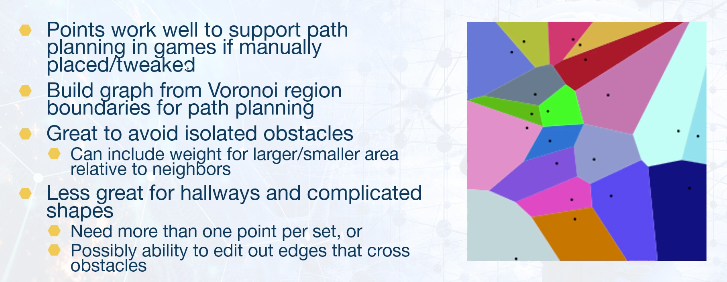
voronoi-dirichlet

voronoi-dirichlet-area

Delaunay Triangulation can be used as it is related to Voronoi Diagram. However, obstacles must be treated as holes and therefore Constrained Edge Delaunay Triangulation Algorithm must be used.

← Path Networks →