What it entails

• Study of algorithms pertaining to geometry
• Motivation for robustness and provable correctness
• Application to discretization
  • Point Containment: If a polygon/region contains a test point
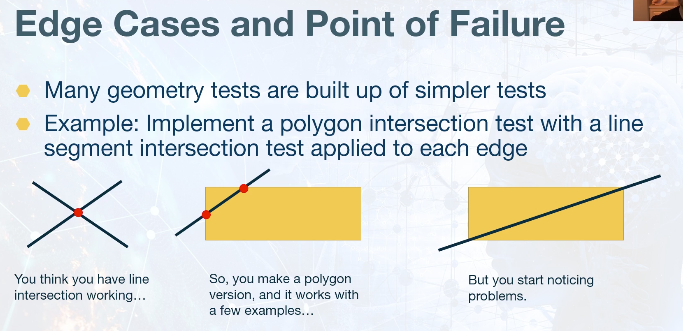
  • Line Intersection
  • Triangulation: Taking a complicated polygon and breaking it down to triangular shapes (think computer graphics)

Floating point vectors problematic

Epsilon solution

Edge cases

Integer Solution

• Converting floats to integers can help support robust computational geometry
• Just multiply each float by some number and cast to an integer (1000 works well for 32-bit ints)
• Floating-point 2d/3d vectors becomes IntVectors
• After computational geometry has been performed, map back to floats
• Conversion to integers can create a lot of overhead and double memory usage.
  • Therefore, if possible, perform this outside of game. Bake computational geometry data structures when building your game.

Integer Representation Problem

• Must be careful with multiplications or sums cause it can lead to overflow
• Can often be proven by considering largest allowed integer in equation terms
• To avoid problem:
  • Reorder equations terms to avoid overflow
  • Process subsets of geometry such that integers fall within a defined safe range
  • Use 64-bit integers or even doubles

Key Takeaways

• Use integer-based algorithms when possible
• Good to avoid angle calculations when you can

Segment Intersection

• segment-intersection-lecture
• line-segment-distance-lecture