Viveckh's Notepad

  • Fuzzy logic incorporate truth degrees, vagueness and subjectivity

  • A linguistic/non-numeric expression of rules and facts.

  • Allows for use of vague human assessments in computing problems.

  • Modeling of imprecise concepts

  • Modeling of imprecise dependencies

  • Superset of classicial logic

  • Introduces concept of degree of membership (DOM)

  • Uses fuzzy sets and fuzzy rules

  • Although it feels probabilityibased, it is NOT.

# Thermostat Example

fuzzy-thermostat-eg.png

# Use cases

  • More direct way to represent expertise in linguistic form. Potential for declarative authoring by non-programmers.
  • Opportunity to capture expertise (of an expert) but lack the resources to train (NN)
  • Flexible behavior design paradigm
  • When behavior design efficiency is more important than optimization
  • Behaviors can act act on multiple variables without imposing rigid structure to decision making

# Golfing Example

fuzzy-golfing-1.png fuzzy-golfing-2.png fuzzy-golfing-3.png

  • NOTE: Lerp refers to linear interpolation function, and Inverse Lerp is the inverse operation of the lerp. Inverse Lerp can be used to determine what the input to a Lerp was based on its output. For example, the value of a Lerp between 0 and 2 with a T value of 1 is 0.5. Therefore the value of an Inverse Lerp between 0 and 2 with a T value of 0.5 is 1.

# Fuzzy Sets

  • Degree of Membership (DOM)
  • Instead of predicates being true or false like in boolean logic, there is a normalized value specifying degree of membership
  • For example: IsInjured(agent) == 0.7. The value is not a probability or a percentage, it is only the degree to which the agent is a member of IsInjured
  • Some traits that one might expect to be mutually exclusive in traditional boolean logic can simultaneously present non-zero degrees of membership. For eg:
    • isHealthy(agent) == DOM(0.3)
    • isInjured(agent) == DOM(0.7)
  • When multiple DOMs are non-zero, it makes sense that DOM should sum to 1.0. However, a weighted average is often sufficient for good results

# Flow

  1. Crisp, discrete input values
  2. Fuzzification
    • Fuzzy boundaries (partial membership) described by "Membership functions"
  3. Fuzzy Rules
    • If antecedent THEN consequent (where antecedent has DOM, and consequent fires by degree)
  4. Defuzzification
    • Combines consequents fired into a crisp value
  5. Crisp, discrete output values

# Fuzzy Inference

  • For each rule,
    • For each antecedent, calculate the degree of membership of the input data
    • Calculate the rule's inferred conclusion based upon the values in previous step
  • Combine all inferred conclusions into a single conclusion (A fuzzy set)
  • For crisp values, the conclusion from 2 must be defuzzified

# Fuzzy Rules

  • Relate the known membership of certain fuzzy sets to generate new DOM values for other (output) fuzzy sets
    • Must create rule for each possible combination of antecedent sets
  • E.g. "If I a close to the corner AND I am traveling fast, then I should brake"
  • Membership of should brake with close-to-corner 0.6 and traveling-fast of 0.9?

# Fuzzification

fuzzy-fuzzification.png

# Example membership functions

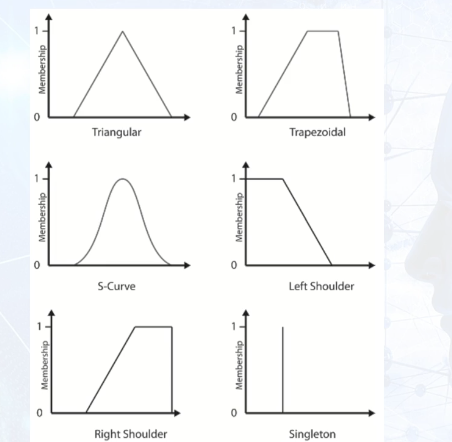
fuzzy-example-memberships.png

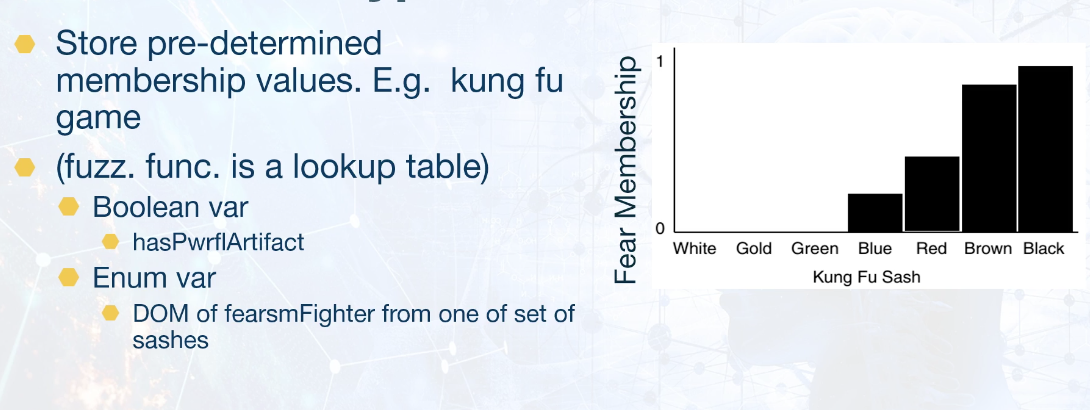
# Small sets and enumerated types

fuzzy-small-sets-fuzzification.png

# Set operations

  • Hedge: VERY =
  • Hedge: FAIRLY =

# Further notes in slides below

← Ballistic Projectiles →