Intercept

Recall Steering Behavior Pursue. An approximate intercept was calculated by estimating how much time it would take for the agent to get in the neighborhood of the target. Using that time estimate, the target's movement could then be extrapolated assuming a constant velocity

Pursue's intercept time is only estimated because it is going to be updated again the next simulation frame and doesn't need to be precise. However, with a ballistic projectile, there is only one chance to get the trajectory correct. Therefore, more computational effort is needed for an accurate trajectory.

• If the target does not move at all and the projectile is constant velocity (not affected by gravity or drag), then only a relative position vector is needed to get launch direction (scale it by desired speed for full velocity)

• The more degrees of freedom (gravity, moving target) allowed, the more complicated the system of equations needed solving gets

Solving

Two general methods to solve

Directly Solve

Formulate a system of equations that represents the problem and directly solve for unknown variables

Iteratively Solve

Estimate a reasonable solution, then refine parameters until the solution is close enough to the desired outcome. To iteratively solve, the movements of projectile and target must be able to be modeled according to the defined parameters.

Static Target

Assume

• 3D positions of projectile and target
• Projectile is affected by gravity (but no drag)
• Projectile will always be launched at full force

What's the direction of the velocity to hit the target (if possible)?

1. Solve for time of collision using quadratic formula. If you are interested in how this equation is derived, lecture videos offer the derivation.

2. Go through the following check list for

3. Solve for using following euqation.

Moving Target / Law of cosines

Assume

• Top-down (XZ plane) with 2D vectors (necessary to reduce complexity so equations are solvable)
• Target and projectile move with constant velocity
• For projectile, only the speed is known

We will see how to adpt 2D solution to 3D, possibly with gravity

1. Solve for the following values that are required to compute velocity

2. Solve for

For 3D

• can be solved with 3D vectors and still get a collision using above equation
• However (y component adds speed)
• This may or may not be acceptable for gameplay (addressed later)

For 3D with gravity

However, this will still have the issues as mentioned earlier in 3D section.

Pros & Cons

• Solves for moving target and can be made to work in 3D with limitations
• Does not guarantee a max speed in 3D
• Not ideal for extreme height differences or target moving significantly with y direction (because 2D logic can't be used in 3D)
• Not ideal for flight sims or space combat

---

Simple Iterative Approach for Static Target Solver

• The method for solving a ballistic trajectory for a static target can be used to aim at moving targets
• An iterative method can leverage the static target solver

Steps

1. Assume target is not moving
2. Solve for projectile intercept of target in step 1.
   • Perhaps use static 3D target method
3. Plug in (might be error, should it be ?) for target's kinematic equation (must be solvable):
   • Possible equation:
4. Now go to 2. but replace target position with
5. Repeat until a terminating condition (like depth count or minimal change in positions)

Tips

• Cap the number of iterations (3-6)
• Preserve previous valid to return if future iterations fail to refine
• Fail immediately if first attempt fails
• Can perform a sanity check on final intercept time by plugging into projectile and target kinematic equations to determine if the iterative estimate is within some minimum distance
• This has added bonus of allowing for shots that are likely to get close enough to a target game object but not necessary hit the center

Pros & Cons

• Easy to implement
• May not be able to refine to a stable solution, especially around point of closest approach or with higher derivatives of motion
• Tends to favor shooting behind target
• Target that is initially unreachable but will be reachable in future creates implementation difficulties
• Doesn't work if kinematic movement of projectile and/or target cannot be directly evaluated (drag and other scenarios)

2D Law of Cosines Iterative

Algorithm

Tips

Follow as the ones suggested in the Simple Iterative Approach above

• XZ vector length for optimal (45 deg.) launch can be solved with Pythagorean Theoream for 45-45-90 triangle.

Pros & Cons

• Finds exact solutions for moving targets
• May miss solutions near the limits
• May not optimize shot for maximum speed and lowest angle (soonest intercept)
• The cons of Simple Iterative Approach do apply as well

Incremental Algorithm

Sometimes projectile and/or target movement can only be modeled incrementally (position/state at current timestep dependent on position/state at previous timestep)

In this case, an incremental algorithm will need to increment through a simplified simulation of projectiles with candidate trajectories and determine the point of closest approach to the target

Millington's book discusses this further.

Practical Issues

With animated characters

• Animation delay from projectile launch (like throwing motion of hand)
• Must make prediction based on when throw will actually happen
• Predict throw from predicted future character position and relative launch position (hand position)

Resource management

• Agent maybe should not waste valuable ammo, or commit to long animation and be unable to throw at a better time
• Implement heuristic for throw decision. Don't throw if conditions are bad.
• Things to consider
  • Is target at top speed? No? Probably accelerating, wait a bit.
  • Target turning? Yes? wait till going straight
  • Is target predicted to hit edge of navmesh? Will likely turn. Lay off throwing
  • Is projectile predicted to hit something sooner than target intercept time? Don't throw.
  • Do you know target's goal? Anticipate arrival at that location

Lobbed projectile collisions

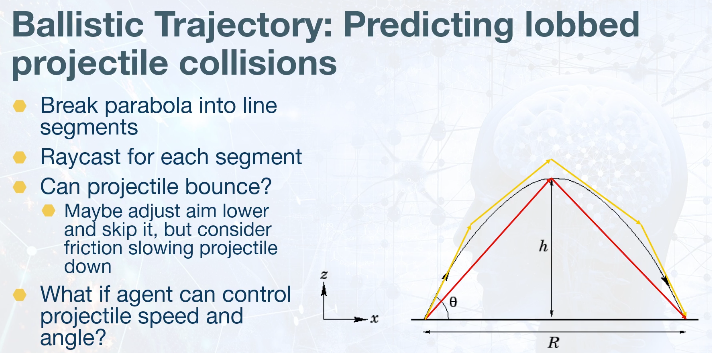
Understanding Equations

• $ This usually represents the norm of a vector. If x = (x1, x2, x3) then ||x|| = (x1^2 + x2^2 + x3^2)^(1/2)

• Unit vector of a vector gives just the direction of the vector. In order to find the vector between two positions, you can do (dest - source) and get the resulting vector. If you only want direction, compute the unit vector of this resulting vector.

• Norm of a vector

• Normalizing a vector

• Direction and Distance from One Object to Another