Mapping trading to RL

• Environment: Market
• State:
  • adjusted close/SMA (using close or SMA by itself however might not be a good choice)
  • Bollinger band value
  • P/E ratio
  • whether we're holding stock
  • return since entry
• Actions: Buy/Sell/Do Nothing
• Reward: Daily Returns (Better cause it is immediate reward), 0 until exit then cummulative return (Delayed reward)

Markov Decision Problems

• Set of states (S)
• Set of actions (A)
• Transition function (T) - [s, a, s']
  • T is a three dimensional object and it records in each cell such that the probabibility if we are in state (s) and action (a), we will end up in state (s')
  • Suppose we are in particular state (s) and take a particular action (a), the sum of all the next states we might end up in (the s's) 1.
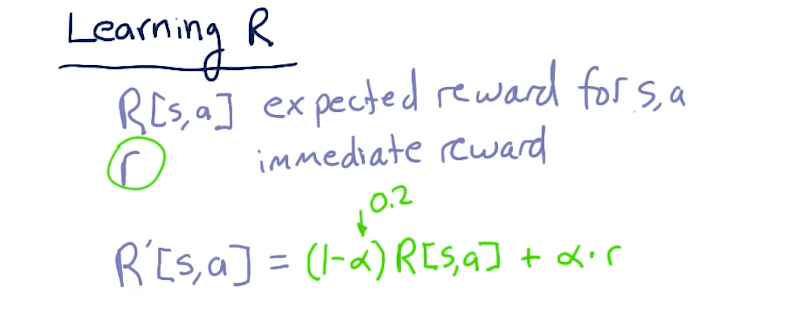
• Reward function (R) - [s, a]
  • If we're in a particular state (s) and we take a particular action (a), we get a reward
• To Find: Policy ((s)) that will maximize reward. If we get the optimal policy, we write it as (s)*

Policy iteration and Value iteration are algorithms that can be used to find the optimal policy.

For trading, since we do not have T amd R, we can't use these Policy iteration and value iteration.

Uknown transitions and rewards

We collect experience tuples

<s1, a1, s1', r1>

<s2, a2, s2', r2>

...

The s1' is the new s2.

Once we gather a trail of experience tuples,

We can use them to compute the Policy

• Model based
  • Build model of T
  • Build model of R
  • Then use value/policy iteration to find optimal policy
• Model free
  • Q-learning

What to optimize?

• Infinite horizon: You'll be collecting reward for infinite time
• Finite horizon: You'll be collecting rewaef for finite reward
• Discounted reward: Time Value of the same reward decreases over time

Q-learning

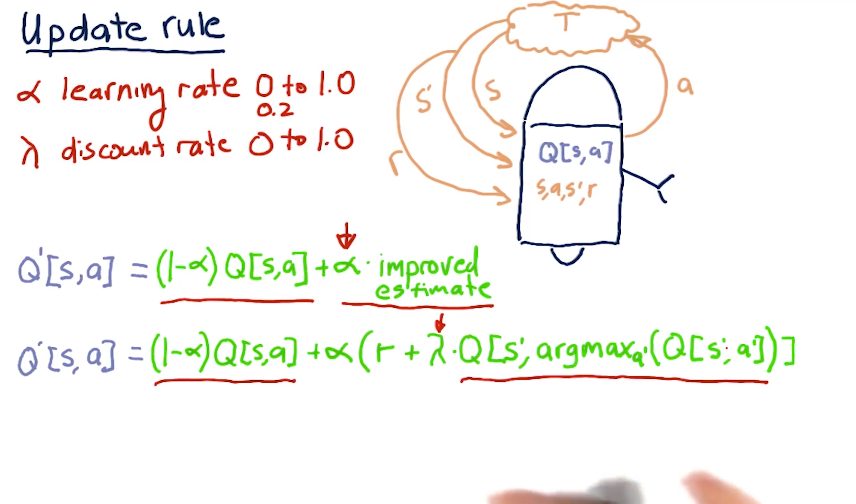
First we have the Q-table

Q[s,a] = immediate reward + discounted reward

How to use Q?

(s) = (Q[s,a])

(s)* = Q*[s,a]

Learning Procedure

Update Rule

Finer Points

• Success depends on exploration
• Choose random action with probability c
  • Coin Flip 1: Are we going to pick random action or action with best Q value?
  • Coin Flip 2: Which of the random actions are we going to select?
  • Picking 0.3 is considered a good value for c

Creating the state

• state is an integer
  • discretize each factor
  • combine each of multiple factors to one integer
  • If the four factors return 0, 4, 2, 6, the single integer for state becomes 0426

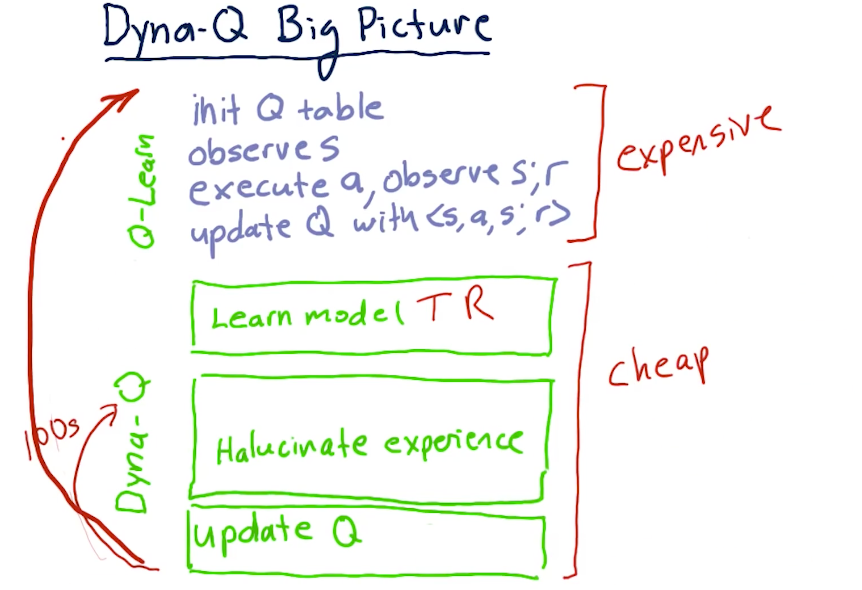
Dyna

Blend of Model-based and Model-free learning.

Since Qlearning does not use T and R, Dyna allows Qlearning to do that.