Localization basics

Maps are described in a global coordinate system, which is independent of a robot’s pose. Localization is the process of establishing correspondence between the map coordinate system and the robot’s local coordinate system. Knowing this coordinate transformation enables the robot to express the location of objects of interest within its own coordinate frame, a necessary prerequisite for robot navigation.

Monte-Carlo Localization / Histogram Filters / Probablistic Localization

The algorithm assumes the Markov property that the current state's probability distribution depends only on the previous state (and not any ones before that),

Probabilistic Localization > Top comment helps visualize

As the number of dimensions increase (2D, 3D, 4D), the number of state variables increase. In case of Histogram filters, this memory scaling is exponential. It is one of the biggest disadvantage of this approach.

Belief

Each cell in the map has an associated prior probability.

Sense

Product of the prior probability with actual sensor measurement. This shall be followed by normalizing the outcome on a scale of 1 to preserve probability

Motion

For each possible location after the motion, we reverse-engineer and guess where the robot could've come from. And then collect the addition of corresponding probabilities.

Mathematically

Using total probability

$p(B) = p(A).p(B|A) + p(\lnot A).p(B| \lnot A)$

Where p(B) is the probability at spot B

p(A) and are the probabilities at positions which could've been possible origins. There could have been more than two, but here we'll look at only two possible origins.

p(B|A) is the probability of ending up at B given prior positioning at A

is the probability of ending up at B given it was not at A

---

The robot could've easily had multiple possible places of origins, in which case, the formula would've looked like:

$p(X) = p(A).p(X|A) + p(B).p(X|B) + p(C).p(X|C) ...$

Problems

Inexact Motion

For a cyclic grid with prior probabilities

Grid Position	1	2	3	4	5
Prior Probability	0	1	0	0	0

And a robot that can jump 1, 2 or 3 cells with following probabilities

$p(x_{i+1} | x_i) = 0.1$

$p(x_{i+2} | x_i) = 0.8$

$p(x_{i+3} | x_i) = 0.1$

Find probability of ending up in pos. 4 given prior probabilities.

SOLUTION

Using concept of total probability from above

$p(x_4) = p(x_3).p(x_4|x_3) + p(x_2).p(x_4|x_2) + p(x_1).p(x_4|x_1)$

$p(x_4) = 0*0.1 + 1*0.8 + 0*0.1 = 0.8$

EXPLANATION: We used the formula of total probability. We are adding up three expressions since the item can end up in position 4 in three possible ways, it can come from position 1, 2 or 3. This is not always the case, but in this case, we are given specific likelihood of the robot being able to jump 1, 2 or 3 positions. Hence, we calculate probability for all those three cases.

---

Exact Motion

For a cyclic world

Grid Position	1	2	3	4	5
Prior Probability	1/9	1/3	1/3	1/9	1/9

And a robot that can only jump 1 cell.

Find probability of ending up in pos. 6.

SOLUTION

Using total probability

$P(6) = P(5).P(6|5) = (1/9) * 1 = 1/9$

EXPLANATION: Since the robot can only jump one cell, the only way it can end up in position 6 is from prior position of 5. Hence P(6|5) can be inferred as 1. The P(5) is the prior probability that is already given as 1/9.

---

The fire problem

P(F)= 0.001, P(Neighbor lie) = 0.1

Deriving, probability of neighbor yelling fire (B) given there is fire, 
since it is just 1 - P(Neighbor lie)
P(B|F) = 0.9 

Non-normalized probability of fire given neighbor cries "fire"

$\bar{P}(F|B) = P(F).P(B|F) = 0.001 * 0.9 = 0.0009$

Non-normalized probability of no fire given neighbor cries "fire"

$\bar{P}(\bar{F}|B) = P(\bar{F}).P(B|\bar{F}) = (1 - 0.001) * 0.1 = 0.0999$

Normalizer - Probability of neighbor yelling "fire!"

$P(B) = 0.0009 + 0.0999 = 0.1008$

Normalized probability of fire given neighbor cries "fire"

$P(F|B) = \frac{ \bar{P}(F|B) }{P(B)} = \frac{0.0009}{0.1008} = 0.0089$

Normalized probability of no fire given neighbor cries "fire

$P(\bar{F}|B) = \frac{ \bar{P}(\bar{F}|B) }{P(B)} = \frac{0.0999}{0.1008} = 0.991$

---

---

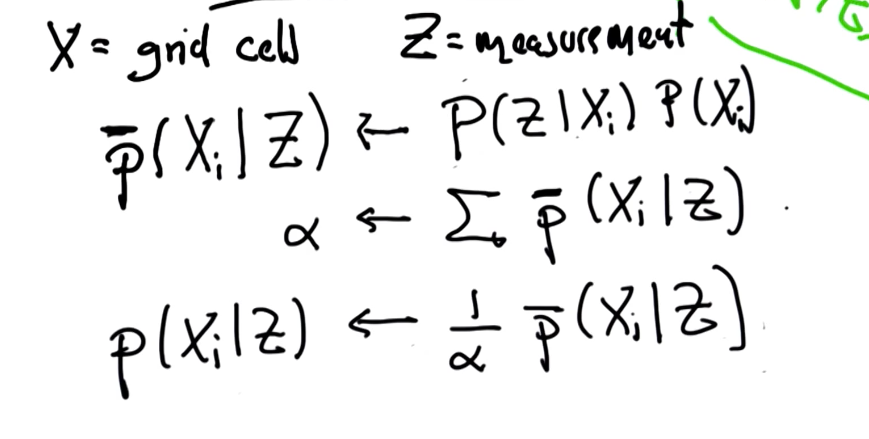
This above concept is broken down in the cancer problem in the lecture - Localization Overvie_Cancer Test_ANS